0. 시작에 앞서
요즘 백준을 통해 알고리즘 문제를 열심히 풀고있다.
문제를 작성하면 내 코드가 다른 사람들의 코드보다 10ms 정도 더 걸리는 경우도 있고,
올바른 답은 나오지만 시간초과로 인해서 문제를 틀리는 경우가 있다.
이럴 때 내 코드가 어떤 시간복잡도를 갖고 있는지를 계산한다면,
개선점을 확인할 수 있을 거라고 생각했다.
그래서 이번 포스팅은 시간 복잡도를 계산하는 방법에 대해서 완전 정복을 해보려고 한다.
1. Big - O 표기법
a) 기본 개념
- 입력값에 따른 알고리즘의 사용량을 예측하는 방법이다.
- 더 자세한 설명을 원한다면, 아래의 링크를 참고하기를 바란다.
https://devraphy.tistory.com/40
Data Structure - 시간 복잡도(Time Complexity)
1. 시간 복잡도 - 어떤 문제를 해결하는데에 있어 어떤 알고리즘이 가장 빠른지 판단하기 위해 알고리즘의 효율성을 수치적으로 계산한 것이다. - 알고리즘의 효율성을 측정하기 위해서 알고리
devraphy.tistory.com
b) O(1) - constant time
- 입력값의 크기에 상관없이 항상 같은 시간이 걸리는 알고리즘
n = input()
if n:
print(True)

c) O(n) - linear time
- 입력값의 크기에 비례해서 처리시간이 증가하는 알고리즘
- 즉, 입력값이 커지면 처리시간도 증가한다.
n = input()
for data in range(len(n)):
print(data)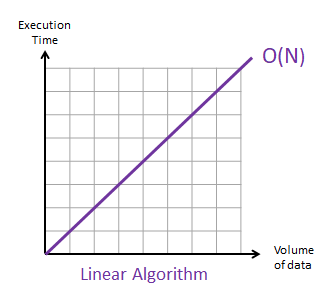
d) O(n의 2승) - quadratic time
- 동일한 반복회수를 갖는 이중 for문이 경우에 해당된다.
- for문 하나당 O(n)의 시간복잡도를 갖는다.
- 이중 for문의 경우 O(n) * O(n) 만큼의 시간복잡도를 갖게 되니까, O(n^2)가 된다.
n = input()
for i in range(len(n)):
for j in range(len(n)):
print(data)
e) O(nm) - quadratic time
- 이중 for문과 동일하지만 서로 다른 횟수를 갖는다.
n = input()
m = input()
for i in range(len(n)):
for j in range(len(m)):
print(data)
f) O(n의 3승) - cubic time
- 삼중 for 문이 여기에 해당한다.
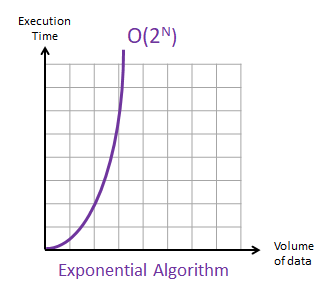
g) O(2의 n승) - exponential time
- 재귀함수로 호출된 피보나치 수열이 여기에 해당된다.
- 재귀함수를 한번 호출할 때마다 2번씩 호출하게 되는 경우를 말한다.
- n은 총 호출되는 수에 따라서(=깊이에 따라서) 달라진다.
def fib(n):
if n == 0:
return 0
elif n == 1 or n == 2:
return 1
else:
return fib(n - 1) + fib(n - 2)- 매번 함수를 호출할 때마다, 재귀함수를 통해 두번씩 호출하게 된다. ex) fib(n-1) 한번, fib(n-2) 두번
h) O(m의 n승) - exponential time
- 재귀함수를 한번 호출할 때마다 m번씩 호출하게 되는 경우를 말한다.
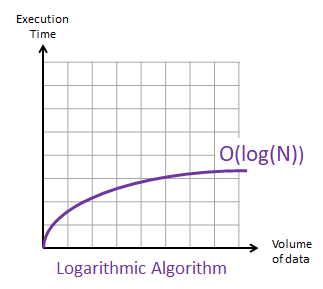
i) O(log n)
- 대표적으로 이진탐색이 O(log n)의 시간복잡도를 갖는다.
- 연산 또는 처리과정을 한번 거칠 때마다 확인해야 하는 절차가 반씩 줄어드는 것을 말한다.
j) O(n의 제곱근) - square root n
- 100의 제곱근(= 루트 100)은 10 이다.
- 제곱근이란, 어떤 값 a를 제곱하여 만들수 있는 수를 말한다.
- 어떤 알고리즘의 모든 경우의 수를 n이라고 해보자.
- n의 제곱근 만큼의 회수를 수행하는 알고리즘의 시간복잡도다.
ex) 모든 경우의 수는 16가지, 실제 수행한 연산의 회수는 4번
k) Big - O 표기법 그래프
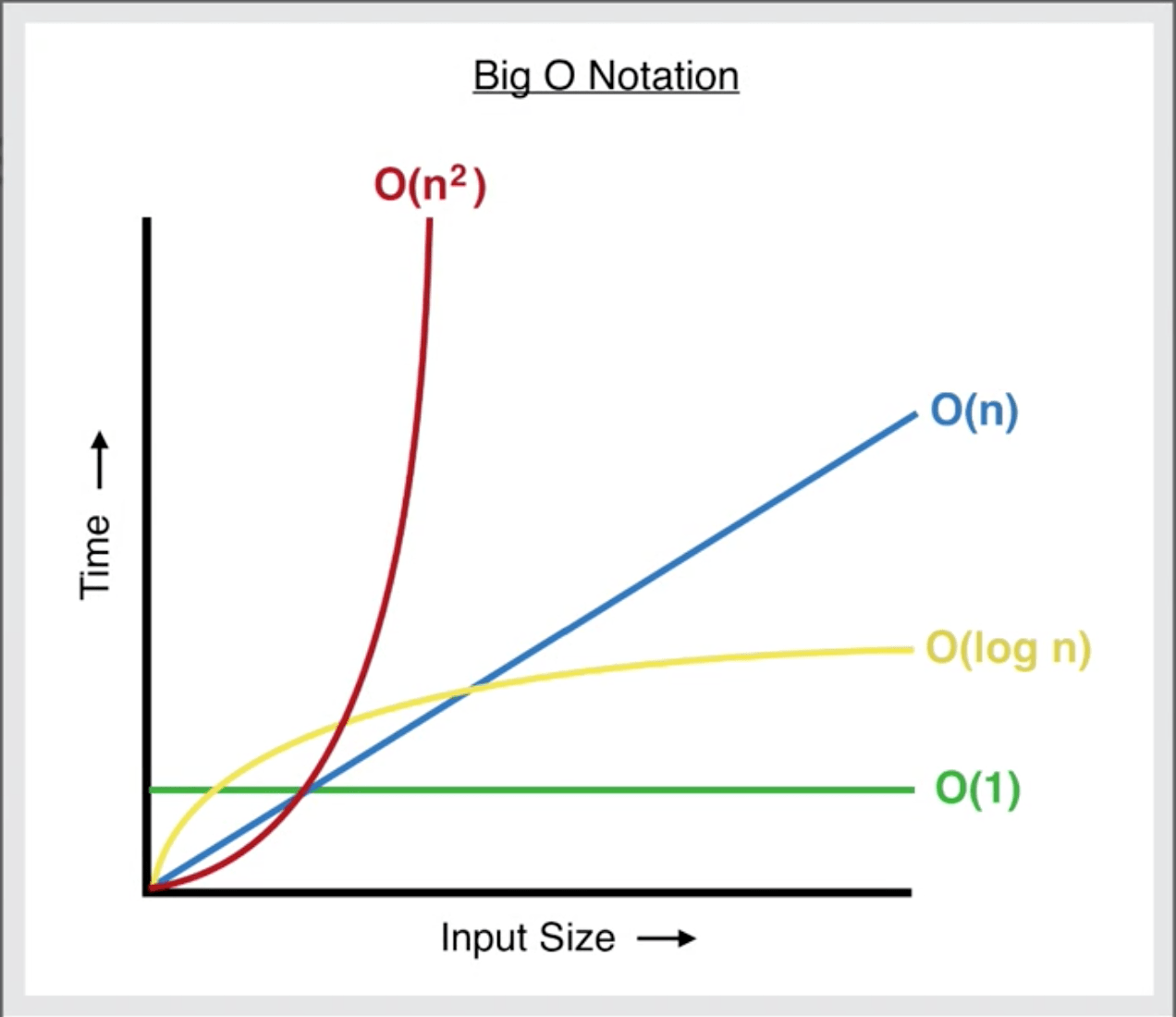
l) Big - O 표기법 랭킹

2. 상수는 버린다.
- 빅 오 표기법에서는 상수를 과감하게 버린다.
- 다음 예시를 살펴보자.
n = input()
for i in range(len(n)):
print(1)
for j in range(len(n)):
print(2)- 위의 알고리즘은 O(2n)만큼의 시간복잡도가 걸린다.
- 그러나 빅 오 표기법에서는 과감하게 2를 버리고 O(n) 만큼의 시간복잡도가 걸린다고 표기한다.
a) 상수를 버리는 이유는?
- 빅 오 표기법은 입력값에 따른 처리시간의 증가율을 예측하기 위한 방법이다.
- 즉, 빅 오 표기법은 실제 알고리즘의 처리시간을 따지는 방법이 아니라는 것이다.
- 상수는 고정된 숫자이기 때문에, 증가율에 따라 고정된 값 만큼의 영향을 미치기 때문에 무시한다.
3. 자료구조 시간복잡도
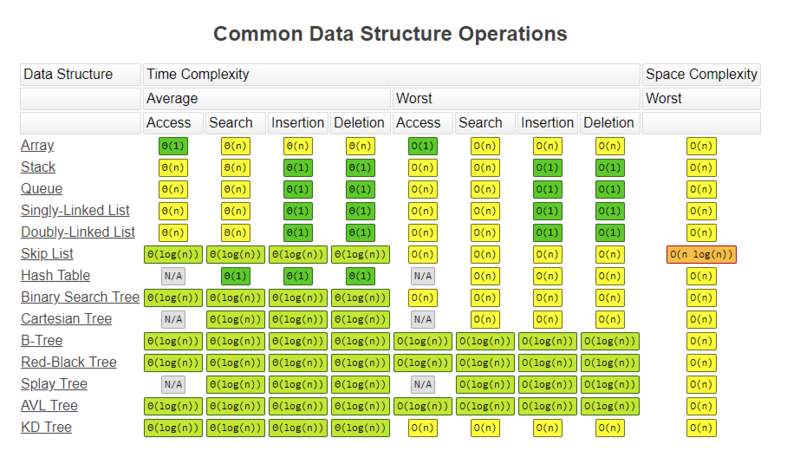
4. 정렬 알고리즘 시간복잡도
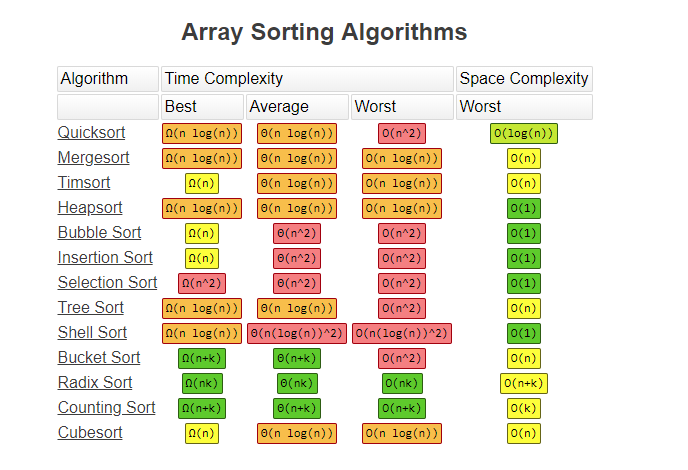
[자료출처]
https://m.blog.naver.com/jhc9639/221339684077
[알고리즘]자료구조에 따른 시간복잡도 O(n) 정리
많이 봤던 그래프입니다. 시간복잡도의 크기에 따라 증가속도를 나타냅니다. n!가 가장 높습니다. 역시 어...
blog.naver.com
https://www.youtube.com/watch?v=6Iq5iMCVsXA
'Algorithm > 알고리즘 공부노트' 카테고리의 다른 글
| 2. Array(배열) - Bubble Sort(버블정렬) (0) | 2021.08.21 |
|---|---|
| 1. Array(배열) - 기본 개념 (0) | 2021.08.20 |
| 파이썬 - filter와 lambda, map 사용방법 (0) | 2021.08.06 |
| 파이썬 배열 - 개념 및 메소드 정리 (8) | 2021.07.30 |
| 입출력과 사칙연산 메소드 정리 (0) | 2021.07.26 |


댓글