1. 개요
- 이전 포스팅에서 보수에 대해서 알아보았다.
- 보수를 이용하여 컴퓨터가 어떻게 정수를 표현하고 계산하는지를 배웠다.
- 이번 포스팅에서는 컴퓨터가 실수를 표현하는 방법을 알아보자.
2. 컴퓨터는 실수를 어떻게 표현할까?
- 사실 컴퓨터는 실수를 정확하게 표현할 수 없다. 즉, 약간의 오차가 있다.
- 왜 그런지 컴퓨터가 실수를 표현하는 방법에 대해서 알아보자.
a) 소수를 이진법으로 바꿔보자.
- 예를 들어, 5.34를 이진법으로 바꿔보자.
- 우선 정수와 소수부를 나누어서 계산한다.
- 5를 이진법으로 바꾸면 101이 된다.
- 소수부 0.34는 다음과 같은 계산을 한다.

- 끝까지 계산해보지는 않았지만, 아마도 무한소수가 될 것 같다.
- 계산 결과를 살펴보면 10100101 어쩌구가 될 것이다.
- 이처럼 컴퓨터가 소수를 표현하는 것은 완벽하지 않고 확실하지 않다.
- 즉, 컴퓨터가 소수를 표현하기 위한 연산에 오차가 존재한다는 것을 이해하자.
- 실수를 표현하는데 발생하는 오차를 최소화 하기위해 사용하는 두가지 표현방식이 있다.
3. 고정 소수점 방식(Fixed Point)
a) 고정 소수점 방식이란?
- 고정 소수점 방식은 말 그대로 소수점의 위치가 고정되어 있는 상태를 말한다.
- 그러므로 고정 소수점은 아래의 사진처럼 역할에 따른 비트의 범위가 고정되어 있다.

- 고정 소수점 방식은 다음과 같이 구성되어 있다.
▶ 음수와 양수를 구분하는 부호
▶ 소수점 이전의 정수를 표현하는 정수부
▶ 소수점 이후의 소수를 표현하는 소수부
b) 고정 소수점의 장단점
▶ 장점
- 제한된 비트 환경에서 실수를 표현하기에 적합하다.
- 표현할 수 있는 수의 범위가 고정되어 있으므로 연산 속도가 빠르다.
▶ 단점
- 각 부분별로 수를 표현할 수 있는 비트의 크기가 고정적이다.
- 표현할 수 있는 수의 범위가 좁다.(=한정적이다)
- 즉, 연산의 정밀도/정확도가 떨어진다. (컴퓨터 내부에서 잘 쓰이지 않는다.)
ex) 소수부가 최대 16비트까지 표현 가능하기 때문에 정확한 수를 표현할 수 없다.
4. 부동 소수점 방식(Floating point)
a) 부동 소수점 방식이란?
- 실수 자료형인 Float이 Floating에서 유래한 것이다.
- 소수점이 여기저기 움직이는 것을 Floating이라고 표현한 것이다.
- 즉, 부동 소수점은 소수점의 위치가 고정되어 있지 않다.
- 그러므로 부동 소수점에서는 실수를 표현하기 위해 정규형을 사용한다.
b) 정규형 - 정규화 표현(Normalized Form)

- 예를 들어, 위의 사진처럼 10진법 실수를 2진법으로 계산한다고 해보자.
- 부동 소수점을 사용하면 위의 사진처럼 지수를 사용하여 소수점의 위치를 표현한다.
- 이렇게 지수를 사용한 소수점의 위치 표현을 만드는데, 그것이 바로 정규형 또는 정규표현이다.
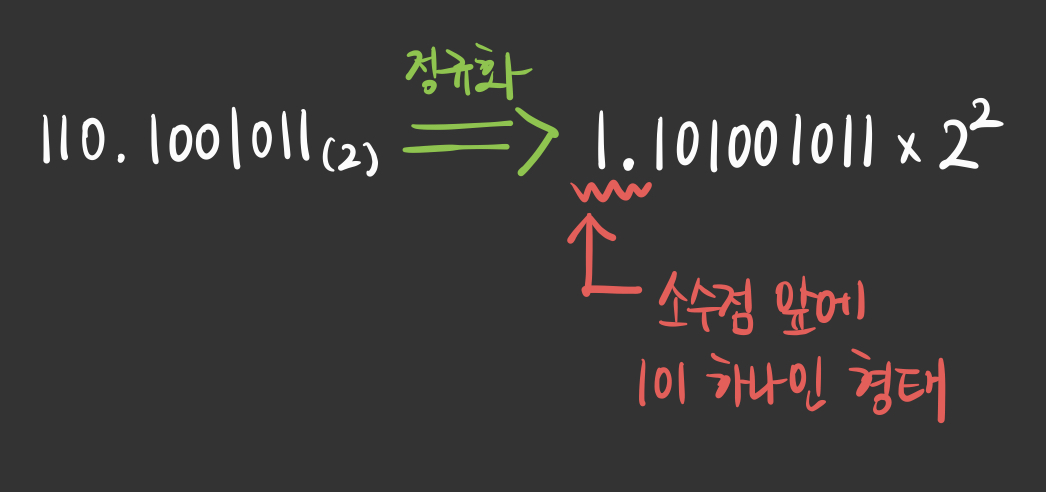
- 정규화란, 소수점 앞에 1이 하나인 형태로 소수점을 이동시켜 표현하는 것이다.
- 이렇게 정규화로 실수를 표현하면 크기비교가 쉽다는 장점이 있다.
- 두 실수를 비교할 때, 지수가 큰 수가 더 큰 수다.
- 지수가 동일하다면, 가수가 큰 수가 더 큰수다.
c) 부동소수점의 표현
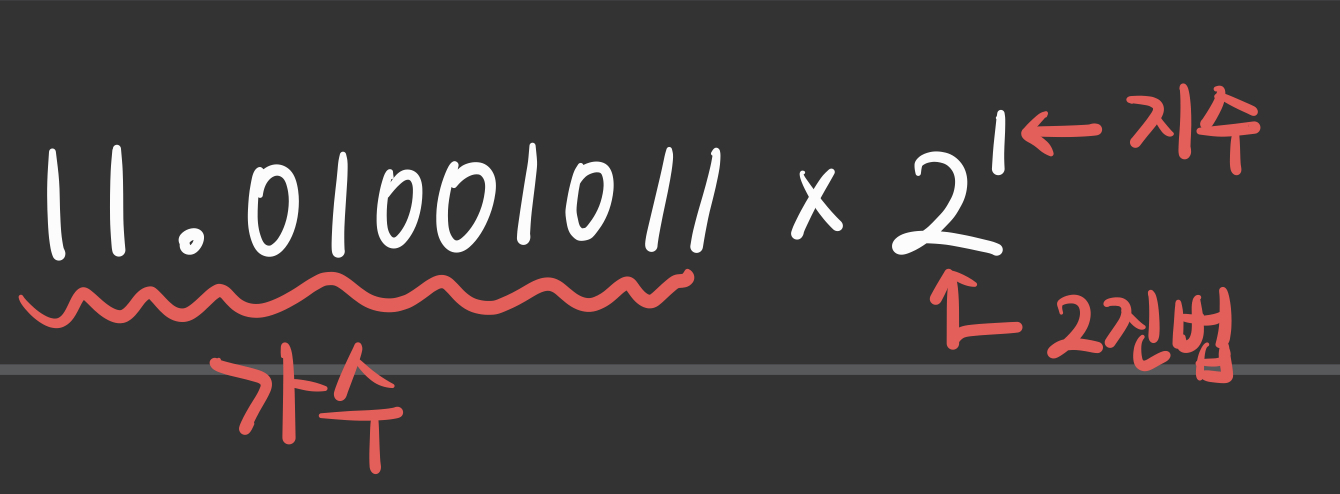

- 부동 소수점 방식은 실수의 정수부와 소수부를 가수부와 지수부로 표현한다.
- 부호 비트도 존재하는데, 이는 가수의 부호를 의미하는 것이다.
- 그러므로 가수는 부호 + 절대값 으로 표현되는 것이다.
- 그렇다면 지수부는 어떻게 표현되는 것일까?
d) 부동소수점 - 지수의 표현
- 부동소수점에서는 지수를 표현할 때, 초과표현을 사용한다.
- 초과표현이란, 말 그래도 얼만큼의 수를 초과시킨다는 것이다.
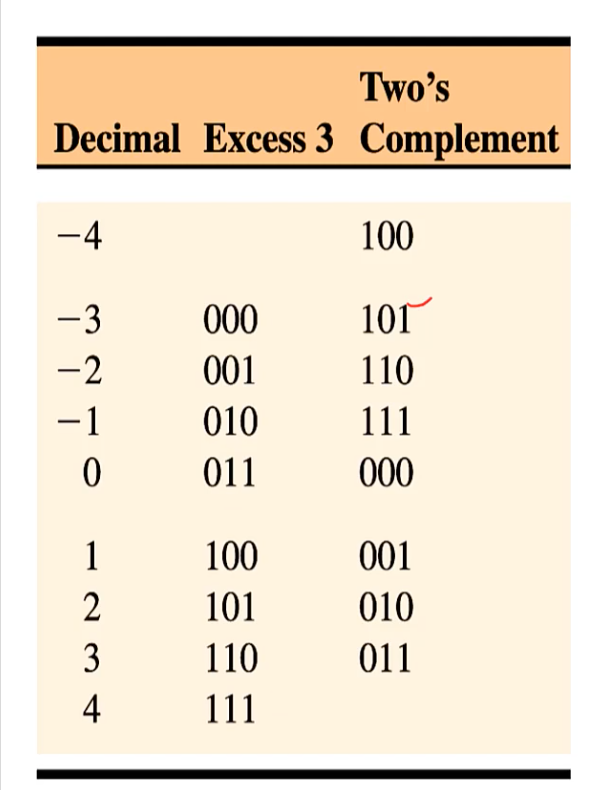
- 만약 지수를 표현하기 위해 3bit를 사용한다면, 3초과 표현을 사용한다.
- 예를 들어, 지수가 -3이라면 3 초과한 0이라고 쓴다.
- 읽을 때에는 0에서 3을 뺀 -3이라고 읽는다.
- 왜 이렇게 복잡한 방법을 쓰는걸까?
d-1) 초과표현(Excess Representation)을 쓰는 이유
- 초과표현을 사용하면 크기를 비교하기가 편하다.
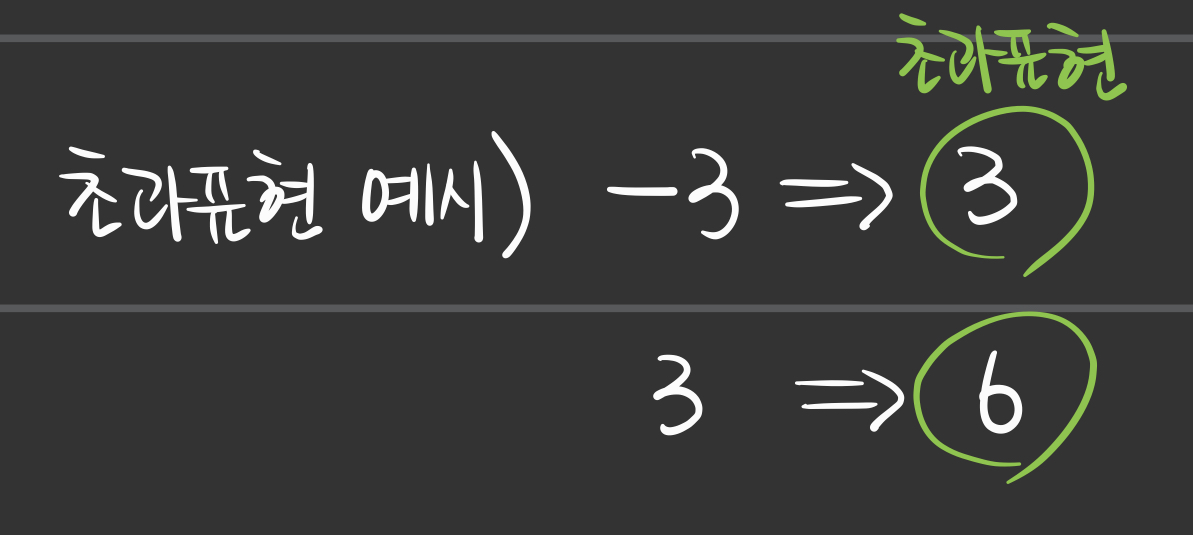
- 위의 예시처럼 부호 판단을 하지 않고 바로 크기를 비교할 수 있다.
- 즉, 초과표현으로 인해서 지수부분만을 이용해 정수의 크기 비교를 할 수 있다.
- 결과적으로, 소수부분의 비교 연산이 필요 없기 때문에 연산 속도가 훨씬 간단하고 빠르다.
d-2) 초과표현을 계산하는 방법
- 지수를 표현하기 위해 몇 비트를 사용하냐에 따라 초과표현이 달라진다.
- 다음 공식을 살펴보자.

- 지수 표현을 몇 비트만큼 사용하는지에 따라 초과표현의 값이 달라진다.

- 예를 들어, 지수 표현을 4bit 만큼 잡는다면 7만큼의 초과표현을 사용하면 된다.
5. 부동소수점을 계산해보자.
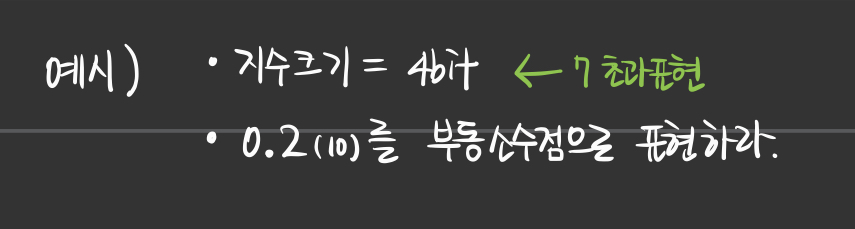


- 위의 그림에 나온 과정을 잘 따라 읽어보자.
- 십진수인 0.2를 부동소수점으로 만들었다.
- 이를 다시 십진법으로 계산해보니 0.195 라는 근사값이 나왔다.
- 이처럼, 컴퓨터에서는 실수를 계산할 때 항상 오차가 발생하며,
- 이를 최소화 하기 위해 사용하는 방식이 부동소수점이다.
6. 부동 소수점 표현 규약(IEEE 754)

▶ 지수비트의 크기가 커진다 = 표현할 수 있는 수의 범위가 넓어진다.
▶ 가수비트의 크기가 커진다 = 실수 표현의 정밀도가 높아진다.
7. 알아두자 - Hidden Bit
- 부동소수점을 만들기 위해 정규화를 하면 반드시 1.xxxx의 형태를 갖는다.
- 이 1을 없애고 소수점의 한자리를 더 표현할 수 있게 하는데, 이때 없어진 1을 Hidden Bit라고 부른다.
- 연산할 때에는 마치 1이 있는 것처럼 연산을 한다.
- 실제로 표현할 때는 1 없이 소수점 자리 하나를 더 표기한다.
a) Zero
- Hidden bit를 사용하면 1이 항상 숨겨져 있다는 전제가 생긴다.
- 0을 표현하기위해 0.0을 입력해도, 이를 0으로 계산하지 않는다.
- Hidden Bit가 있다고 계산하기 때문이다.
▶ 약속을 통한 0의 표현
- 그러므로 0 0000 0000을 0으로 하기로 약속했다.
- 이로 인해서 다음과 같은 추가적인 규칙이 파생된다.
- 가장 작은 양수 = 0 0000 0001
- 가장 큰 양수 = 0 1111 1111
8. 알아두자 - Out of Range
- 총 8비트를 이용하여 실수를 표현한다고 할 때,
- 부호(1비트) / 지수(3비트) / 가수(4비트)로 구성하게 된다.
- 이렇게 구성하면 다음과 같은 표현의 범위를 갖는다.
▶ 양의 실수 표현범위: 0.1328125 ~ 31.0
▶ 음의 실수 표현범위: -31.0 ~ -0.1328125
▶ 두 범위의 사이에 0은 약속에 의해 존재한다.
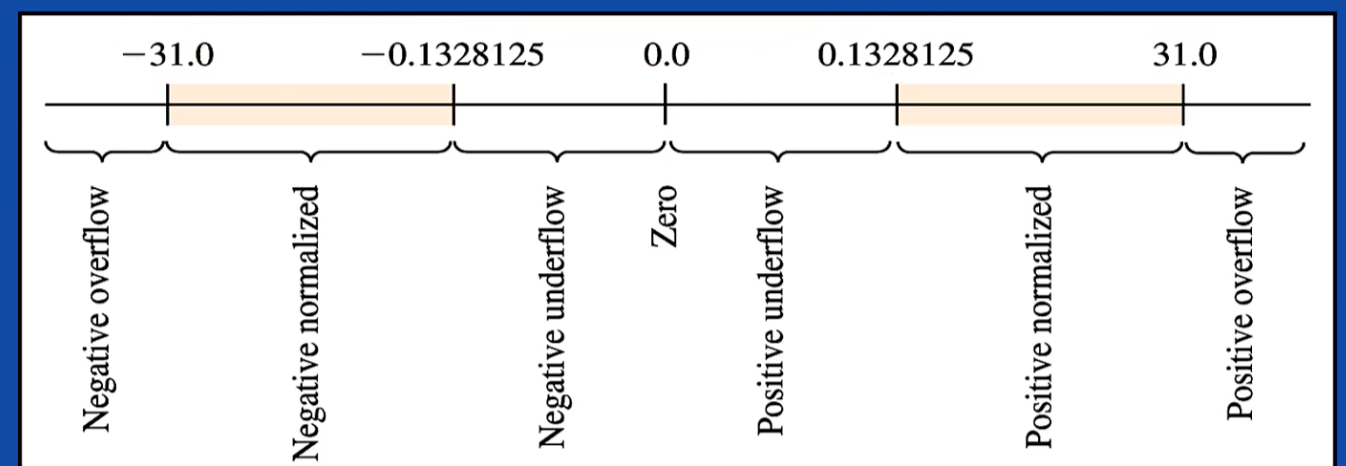
▶ 양수의 최대값(31.0)보다 큰 수를 표현하면 Overflow
▶ 양수의 최소값(0.1328125)보다 작은 수를 표현하면 Underflow
▶ 음수의 최소값(-31.0)보다 작은 수를 표현하면 Overflow
▶ 음수의 최대값(-0.1328125)보다 큰 수를 표현하면 Underflow
- 정수에는 Overflow라는 개념만 존재하지만, 실수에는 Over/Underflow 모두 존재한다.
9. 총 정리 및 요약

[자료출처]
'컴퓨터공학기초 개념 > 컴퓨터구조' 카테고리의 다른 글
| 9. 논리회로 - 논리 게이트(logical gate) (1) | 2021.08.05 |
|---|---|
| 8. 데이터 표현 - BCD, 패리티 비트, 해밍코드 (0) | 2021.08.05 |
| 6. 데이터 표현 - 2의 보수를 사용하는 이유 (3) | 2021.08.03 |
| 5. 데이터 표현 - 2의 보수 (Two's complement) (0) | 2021.08.03 |
| 4. 데이터 표현 - 1의 보수(one's complement) (0) | 2021.08.03 |




댓글