1. Heap이란?
- Heap은 트리구조를 기반으로한 자료구조로 데이터에서 최대값과 최소값을 빠르게 찾기위해 고안된 완전 이진트리(Complete Binary Tree)이다.
* 완전이진트리란?
→ 트리에 데이터가 삽입될 때, 왼쪽에 위치한 자식노드를 먼저 채우는 규칙을 갖고 있는 이진트리이다. 이진트리이기 때문에 자식노드는 2개만 가질 수 있다.
1) Heap을 사용하는 이유
- 우선순위 큐와 같이 최대값과 최소값을 빠르게 찾기위해 사용한다.
- 이를 배열로 구현하면 최대값과 최소값을 찾는데 O(n)만큼 걸린다.
- 반면에, heap을 이용하여 최대값과 최소값을 찾으면 O(log n)만큼 걸린다. (더 빠르다)
2) Heap의 구조
- Heap은 최대/최소 값을 구하기 위한 구조인 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 분류할 수 있다.
- Heap은 다음과 같은 조건을 갖고 있는 자료구조이다.
- Max Heap의 경우, 각 노드의 값은 해당 노드의 자식노드가 가진 값보다 크거나 같다. 즉, 부모가 되는 노드가 자식노드보다 크거나 같은 값을 갖는다.
- 반대로 Min Heap의 경우, 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 작거나 같다. 즉, 부모가 되는 노드가 자식노드보다 작거나 같은 값을 갖는다.
- Heap은 완전이진트리의 형태를 갖는다.
- 위의 조건에 의해, Heap의 루트노드는 반드시 최대/최소값을 갖고 있게 된다.
3) Heap과 이진탐색트리의 공통점과 차이점

- 공통점
a) Heap과 이진탐색트리 모두 이진트리를 기반으로 하고있다. (자식노드가 최대 2개) - 차이점
a) Heap은 부모노드의 값이 가장 크거나 같다(또는 가장 작거나 같다) 그러므로 자식노드 간의 크기비교에 대한 규칙이 존재하지 않는다. 반면에, 이진탐색트리는 왼쪽 자식노드(가장 작음) < 부모노드 < 오른쪽 자식노드(가장 큼) 순으로 구조를 이룬다.
b) 이진탐색트리는 탐색(검색)을 위한 구조이며, Heap은 최대/최소값을 검색하기 위한 구조이다.
2. Heap의 기본동작 - 데이터 삽입
- Heap은 완전이진트리이므로, 왼쪽 최하단 노드부터 채워지는 형태로 데이터가 삽입된다.
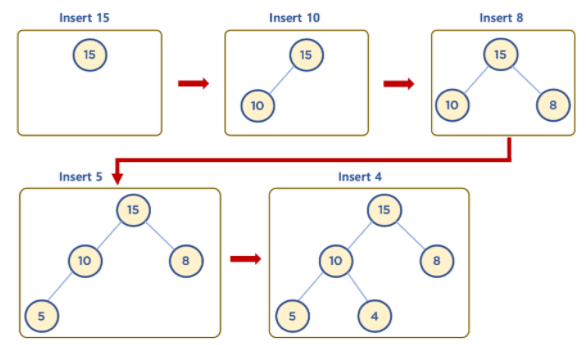
- 위의 사진은 기존의 데이터보다 작은 데이터가 삽입될 때 동작하는 방식이다. 만약에 기존 데이터들보다 큰 데이터가 삽입될 경우에는 어떻게 동작할까? (아래 사진참고)
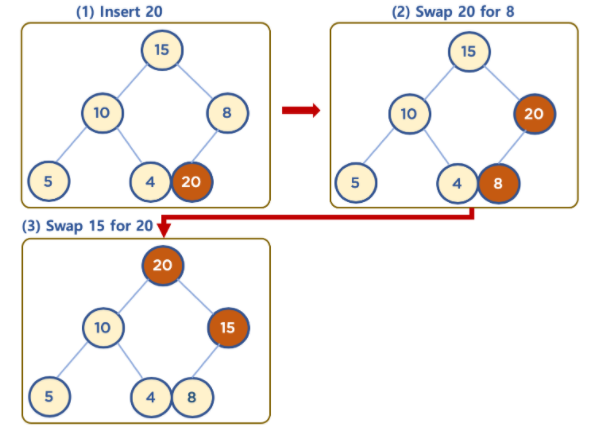
- 기존의 데이터 중 가장 큰 수는 15. 하지만, 새로 삽입될 데이터는 20이다. 이런 경우 위의 사진과 같은 과정을 거치게된다.
(1) 먼저 삽입된 데이터들의 완전이진트리 구조에 맞추어 좌측 최하단부의 노드에 데이터(20)를 삽입한다.
(2) 삽입 후, 삽입된 데이터가 자신의 부모 노드보다 값이 클 경우에 자리를 바꿔주는 작업을 한다. 이를, Swap이라고 한다.
(3) 부모노드가 더 큰 값이 나올 때까지 2번 과정을 반복한다. 새로 삽입된 데이터가 root 노드가 될 경우, swap을 멈춘다.
3. Heap의 기본동작 - 데이터 삭제
- Heap은 최대 또는 최소값을 추출하기 위해 사용한다. 그렇기 때문에, 최대값 또는 최소값이 위치하는 최상단 노드(root)를 삭제하는 것이 일반적이다.
- root 노드가 삭제(추출)되고 나서 좌측 최하단에 위치한 노드(= 일반적으로 가장 나중에 삽입된 노드)를 root로 이동시킨다. 이 후, root노드를 기준으로 자식노드와 비교하여 가장 큰 값을 찾아 root노드와 위치를 바꾸는 작업(swap)을 반복한다. 이를 더이상 자식노드가 없을 때까지 수행한다. (아래 사진참고)
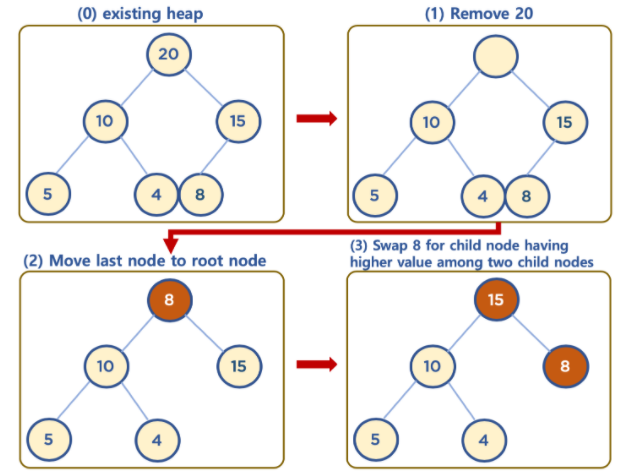
4. Heap의 규칙성
- Heap은 완전이진트리 구조이기 때문에 일반적으로 배열을 이용하여 구현한다. (데이터 저장순서가 있기 때문)

- 배열은 인덱스가 0번부터 시작하지만, Heap구현의 편의를 위해 0번을 비워두고 root 노드를 1번으로 지정하여 구현한다. 이렇게 구현하면 어떤 노드의 번호를 알게 되면 부모노드가 몇번인지 쉽게 알 수 있다. 이게 어떤 의미인지 알아보자.
1) Heap의 규칙성
- 부모노드의 인덱스 번호는 자식노드의 인덱스번호를 2로 나눈것의 몫(//) 이다. 여기서 2로 나누는 이유는 자식노드가 최대 2개까지만 존재하는 Heap의 완전이진트리 구조를 이용한 것이다. 위의 사진을 기반으로 설명하겠다.
* // 연산자는 몫을 구하는 연산자이다.
ex) 5번 노드의 부모 노드를 알고 싶다면 5/2의 몫 즉, 2가 되는 것이다. → 5//2
ex) 3번 노드의 부모 노드를 알고 싶다면 3/2의 몫 즉, 1이 되는 것이다. → 3//2
- 이러한 규칙성을 기반으로 Heap의 인덱스 번호를 구하기 위해 알아야 할 3가지 공식이 있다.
1. 부모 노드의 인덱스 = 자식노드 인덱스 // 2
2. 좌측 자식 노드의 인덱스 = 부모 노드 인덱스 * 2
3. 우측 자식 노드의 인덱스 = 부모 노드 인덱스 * 2 + 1 (사칙연산은 곱셉과 나눗셈을 우선시 한다)
4. Heap 구현
1) Heap 클래스 및 객체 생성
class Heap:
def __init__(self, data):
self.heap_array = list() # 배열(=리스트) 구조로 선언
self.heap_array.append(None) # 0번 인덱스를 비우는 작업
self.heap_array.append(data)heap = Heap(1) # 객체 생성
heap.heap_array # 출력 및 확인
[출력 결과]

2) Heap 메소드 - insert()
# 2) 마지막에 삽입된 데이터의 index를 확인하여
# 순서정렬 필요를 확인하는 메소드
def move_up(self, inserted_index):
# 데이터가 없다면 삽입될 데이터가 root노드가 되기에 순서정렬 불필요
if inserted_index <= 1:
return False
else:
parent_index = inserted_index // 2
# 삽입된 값이 부모노드보다 큰 값인지 비교
if self.heap_array[inserted_index] > self.heap_array[parent_index]:
return True
else:
return False
def insert(self, data):
# 1) 데이터 추가
# Heap 객체(배열)에 데이터가 없는 경우
if len(self.heap_array) == 0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
# Heap 객체(배열)에 데이터가 있는 경우
self.heap_array.append(data)
# 3) 데이터 순서 정렬
inserted_index = len(self.heap_array) - 1 # 가장 마지막에 삽입된 데이터 찾기
while self.move_up(inserted_index): # True = 순서정렬이 필요
parent_index = inserted_index//2 # 부모노드의 index를 알아냄
# 위치를 바꿔줌. a:b = c:d의 구조로 서로 대응하는 값을 바꿔주는 알고리즘
self.heap_array[inserted_index], self.heap_array[parent_index] = self.heap_array[parent_index], self.heap_array[inserted_index]
inserted_index = parent_index #index 또한 바꿔준다.
return True
3) 전체 코드
class Heap:
def __init__(self, data):
self.heap_array = list() # 배열(=리스트) 구조로 선언
self.heap_array.append(None) # 0번 인덱스를 비우는 작업
self.heap_array.append(data)
# 2) 마지막에 삽입된 데이터의 index를 확인하여
# 순서정렬 필요를 확인하는 메소드
def move_up(self, inserted_index):
# 데이터가 없다면 삽입될 데이터가 root노드가 되기에 순서정렬 불필요
if inserted_index <= 1:
return False
else:
parent_index = inserted_index // 2
# 삽입된 값이 부모노드보다 큰 값인지 비교
if self.heap_array[inserted_index] > self.heap_array[parent_index]:
return True
else:
return False
def insert(self, data):
# 1) 데이터 추가
# Heap 객체(배열)에 데이터가 없는 경우
if len(self.heap_array) == 0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
# Heap 객체(배열)에 데이터가 있는 경우
self.heap_array.append(data)
# 3) 데이터 순서 정렬
inserted_index = len(self.heap_array) - 1 # 가장 마지막에 삽입된 데이터 찾기
while self.move_up(inserted_index): # True = 순서정렬이 필요
parent_index = inserted_index//2 # 부모노드의 index를 알아냄
# 위치를 바꿔줌. a:b = c:d의 구조로 서로 대응하는 값을 바꿔주는 알고리즘
self.heap_array[inserted_index], self.heap_array[parent_index] = self.heap_array[parent_index], self.heap_array[inserted_index]
inserted_index = parent_index #index 또한 바꿔준다.
return True
[테스트 결과]

'컴퓨터공학기초 개념 > 알고리즘 개념' 카테고리의 다른 글
| Data Structure - 개념 정리(summary) (0) | 2020.09.08 |
|---|---|
| Data Structure - Heap(2) (0) | 2020.09.03 |
| Data Structure - 트리(Tree) & 이진탐색트리(Binary Search Tree) (0) | 2020.08.26 |
| Data Structure - Hash Table (2) (0) | 2020.08.22 |
| Data Structure - Hash Table (1) (0) | 2020.08.22 |



댓글