0. 문제
https://leetcode.com/problems/01-matrix/
01 Matrix - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
1. 문제 설명
- 문제에서 이중 배열(mat)이 주어진다.
- 이중 배열의 원소 중 1이 입력된 위치를 찾고, 해당 위치부터 0까지의 최단 거리를 찾아낸다.
- 최단 거리가 잘못 입력된 원소를 수정하여 올바른 값을 가진 이중 배열을 반환하는 것이 이 문제의 핵심이다.
2. 문제 해설
- 글쓴이는 이 문제를 풀기까지 이틀의 시간이 필요했다.
- 대표적으로 2가지 해결책이 존재하지만, 왜 그러한 접근법이 필요한지 이해하지 못했기 때문이다.
- 이번 포스팅에서는 2가지 해결책을 설명하고, 왜 이러한 해결책이 필요한지 설명할 예정이다.
a) 첫 번째 접근 - 1을 기준으로 0 찾기
- 우선 이중 배열을 탐색하면서 1의 위치를 찾는다.
- 1의 위치를 기준으로 0까지의 거리를 찾기 위해 재귀로 탐색을 구현한다.
- 그러나 이 방법은 해결책이 되지 못한다.
- 탐색의 시작점을 1의 위치로 잡으면 StackOverflow가 발생하기 때문이다.
- 다음 예시 코드를 살펴보자.
class Solution {
int count = 0;
public int[][] updateMatrix(int[][] mat) {
int row = mat.length;
int col = mat[0].length;
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(mat[i][j] == 1) {
mat[i][j] = findZero(mat, i, j);
}
}
}
return mat;
}
public int findZero(int[][] mat, int row, int col) {
if(row < 0 || col < 0 || row >= mat.length ||
col >= mat[0].length || mat[row][col] == 0) {
int temp = count;
count = 0;
return temp;
}
count ++;
return 1 + Math.min(
Math.min(findZero(mat, row - 1, col),findZero(mat, row + 1, col)),
Math.min(findZero(mat, row, col - 1), findZero(mat, row, col + 1)));
}
}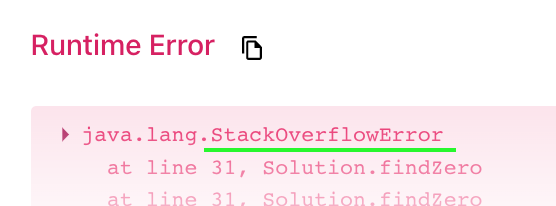
- 솔직히 위의 코드가 올바른 답을 반환하는지는 알 수 없다.
- 그러나 메모리를 초과하는 연산이므로, 올바른 접근이 아니라는 것은 확실하다.
- 그렇다면 메모리가 초과하는 이유는 무엇일까?
- 문제의 제약에는 다음과 같이 적혀있다.
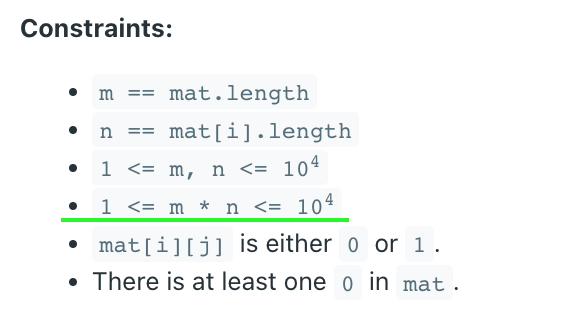
- 이중 배열은 최대 10000개의 원소를 가질 수 있다.
- 1의 위치를 발견할 때마다 0까지의 최단 거리를 찾기 위해 이중 배열 전체의 원소를 탐색한다.
- 1만 개의 원소를 가진 이중 배열이 주어진다면 매번 1만 개의 원소를 탐색하는 것이다.
- 즉, 1의 총 개수 * 1만 개의 원소를 탐색해야 한다.
- 뿐만 아니라 어떤 원소 1부터 어떤 원소 0까지의 경로는 1개가 아니다.
- 즉, 탐색해야 하는 경로의 수는 1만 가지 이상이 될 수 있다는 것이다.
- 여기서 StackOverflow가 발생한다.
b) 두 번째 접근 - 메모리 초과의 발생 원인
- 이제 1을 기준으로 접근하면 이 문제를 해결할 수 없다는 것을 확인했다.
- 그렇다면 무엇을 기준으로 최단 경로를 찾아야 할까?
- 역으로 0을 기준으로 1까지의 거리를 찾으면 된다.
- 1을 기준으로 탐색하면 메모리가 초과되는데, 왜 0을 기준으로 탐색하면 해결할 수 있을까?
- 이 부분이 글쓴이가 가장 고뇌한 부분이다. 잘 이해가 가지 않았다.
- 단편적인 예를 통해 그 이유를 알아보자.
- 다음 그림은 2를 기준으로 0까지의 최단거리를 찾기 위해 탐색하는 경로다.

- 이처럼 2를 기준으로 0까지 탐색할 수 있는 경로는 총 5가지다.
- 반대로, 0을 기준으로 2까지 탐색하는 경우를 살펴보자.
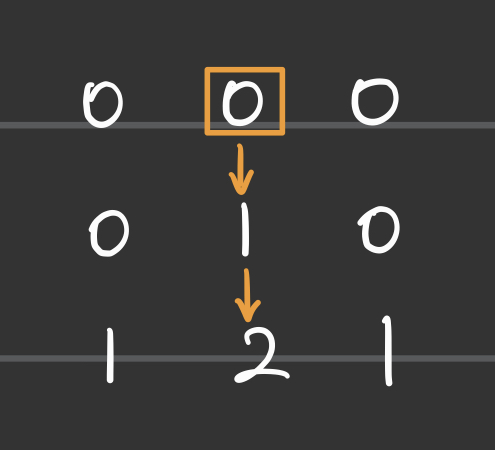
- 0을 기준으로 2까지 탐색하는 경로는 1개다.
- 2행 3열의 0을 기준으로 2까지의 경로를 탐색하더라도 총경로는 2개다.
- 이처럼 0을 기준으로 1을 탐색하는 것이 훨씬 효율적이다.
- 여기서 효율적이다는 의미는 탐색해야 하는 경로의 수가 현저히 적다는 것이다.
c) 세 번째 접근 - 0을 기준으로 1을 찾는 방법
- 이제 0을 기준으로 탐색하는 코드를 작성해보자.
- 0을 기준으로 탐색할 때 중요한 점은 양방향으로 검증해야 한다는 것이다.
- 그 이유는 문제에서 최단 거리를 찾기 때문이다.
- 다음 예시를 살펴보자.
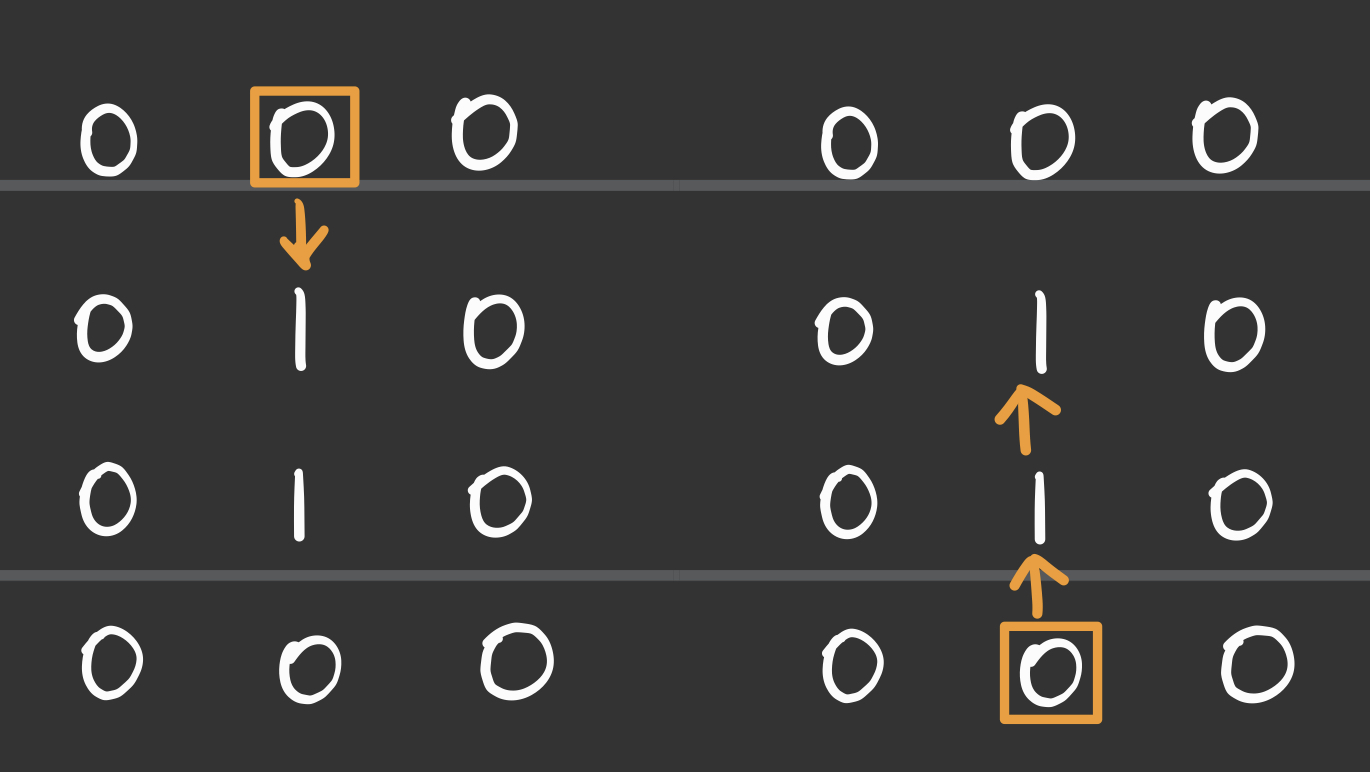
- 왼쪽의 예시는 1행 2열에 위치한 0을 기준으로 2행 2열에 위치한 1까지의 경로다.
- 오른쪽의 예시는 4행 2열에 위치한 0을 기준으로 2행 2열에 위치한 1까지의 경로다.
- 위쪽에서 탐색할 때는 경로가 1이지만, 아래쪽에서 탐색할 때는 경로가 2다.
- 이처럼 0을 기준으로 검증할 때에는 방향성에 따라 경로가 달라지므로 양방향 검증을 해야 한다.
- 즉, 서로 다른 방향의 단방향 탐색을 2번 수행하여 최단 거리를 찾아내는 방식이다.
- 이 방식은 이중 for문을 2번 구현하여 해결할 수 있다.
d) 네 번째 접근 - BFS를 사용한 탐색
- 또 다른 해결 방식은 0을 기준으로 BFS를 수행하는 방식이다.
- 이는 전통적인 BFS를 수행하는 방식으로, 이중 배열을 그래프라고 생각하면 이해가 편하다.
- BFS이므로 방문해야 할 노드를 기록하는 Queue 자료구조가 필요하다.
- 그리고 최단 거리를 기록할 이중 배열(= dist)이 필요하다.
- 시작점이 0이므로 이중 배열을 탐색하면서 모든 0의 위치를 Queue에 저장한다.
- 1의 위치가 발견되면, 이는 dist에 최대 값으로 저장한다.
→ 여기서 최대 값은 문제에서 원소가 가질 수 있는 최대 값보다 큰 수를 사용한다.
→ 아래의 예시에서는 Integer.MAX_VALUE를 사용하였다.
- 이 과정을 거치면 다음과 같은 결과를 만든다.

- 이로써 검증해야 할 모든 시작점(= 0)의 위치는 Queue에 저장되었다.
- Queue에 저장된 모든 위치는 방문해야 할 위치가 된다.

- Queue에 저장된 시작점을 하나씩 뽑아서 이중 배열(= dist)의 탐색을 시작한다.
- 시작점의 위치를 기준으로 상하좌우에 인접한 노드가 있는지 확인한다.
- 시작점을 기준으로 상하좌우를 탐색 시, 다음 2가지 조건을 검사한다.
→ 탐색 위치가 행열의 범위를 벗어나는지 확인한다.
→ 탐색 위치의 dist 값이 시작점의 값 + 1 보다 큰 경우, 해당 위치의 dist 값을 시작점의 값 + 1로 수정한다.

- 최초에 시작점은 0이다. 그러므로 탐색한 위치의 값이 0이 아니라면, 시작점을 기준으로 탐색 위치는 1칸 떨어진 것이다.
- 탐색 위치의 값과 시작점의 값 + 1을 비교하는 이유는 최초에 시작점의 값이 0이기 때문이다.
- 위에서 dist에는 1이 발견된 위치에 최대 값을 저장하였다.
- 즉, 시작점의 값 + 1보다 큰 수가 발견되었다는 것은 1이 발견됐다는 의미다.
- 이처럼 시작점보다 큰 값이 발견되면, 해당 위치의 값을 시작점 + 1로 수정한다.
- 탐색 위치의 값이 0이 아니므로 해당 위치의 주변은 탐색의 대상이 된다.
- 그러므로 현재 탐색 위치는 Queue에 저장된다.

- 이 과정을 반복하면 최단 거리를 찾아낼 수 있다.
- 다음 코드를 보면서 이해해보자.
3. 정답 코드
a) 이중 for문을 사용한 양방향 검증
class Solution {
public int[][] updateMatrix(int[][] mat) {
int row = mat.length;
int col = mat[0].length;
int[][] result = new int[row][col];
int maxDistance = (row - 1) + (col - 1);
// 위에서 아래로 검증
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(mat[i][j] != 0) {
int upper = (i > 0) ? result[i - 1][j] : maxDistance;
int left = (j > 0) ? result[i][j - 1] :maxDistance;
result[i][j] = Math.min(upper, left) + 1;
}
}
}
// 아래에서 위로 검증
for(int i = row - 1; i >= 0; i--) {
for(int j = col - 1; j >= 0; j--) {
if(mat[i][j] != 0) {
int bottom = (i < row - 1) ? result[i + 1][j] : maxDistance;
int right = (j < col - 1) ? result[i][j + 1] : maxDistance;
result[i][j] = Math.min(Math.min(bottom, right) + 1, result[i][j]);
}
}
}
return result;
}
}
b) BFS 방식
class Solution {
public int[][] updateMatrix(int[][] mat) {
int row = mat.length;
int col = mat[0].length;
int[][] dist = new int[row][col];
int[][] directions = {{1,0}, {0,1}, {-1,0}, {0,-1}};
Queue<int[]> que = new LinkedList<>();
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(mat[i][j] == 0) {
que.offer(new int[]{i,j});
}
else {
dist[i][j] = Integer.MAX_VALUE;
}
}
}
while(!que.isEmpty()) {
int[] position = que.poll();
int x = position[0];
int y = position[1];
for(int[] direction : directions) {
int newX = x + direction[0];
int newY = y + direction[1];
if(newX >= 0 && newY >= 0 && newX < row && newY < col &&
dist[newX][newY] > dist[x][y] + 1) {
que.offer(new int[]{newX,newY});
dist[newX][newY] = dist[x][y] + 1;
}
}
}
return dist;
}
}
'Algorithm > 알고리즘 문제풀이' 카테고리의 다른 글
| LeetCode 77(Combinations, java) (0) | 2022.05.06 |
|---|---|
| LeetCode 994(Rotting Orange, java) (0) | 2022.05.06 |
| LeetCode 116(Populating Next Right Pointers in Each Node, java) (0) | 2022.04.29 |
| LeetCode 617(Merge Two Binary Trees, java) (0) | 2022.04.28 |
| LeetCode 695(Max Area of Island, java) (0) | 2022.04.27 |




댓글