1. 선택 정렬(Selection Sort) 이란?
- 주어진 데이터 중, 최소값을 찾아 순서대로 나열하는 정렬방법
- 찾아낸 최소값을 데이터의 맨 앞에 위치한 값과 교체한다.
- 교체된 맨 앞의 최소값을 제외한 나머지 데이터를 대상으로 이전의 작업을 반복한다.
- 최종적으로 정렬된 데이터의 구조를 갖는다.
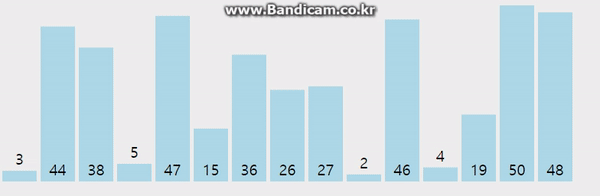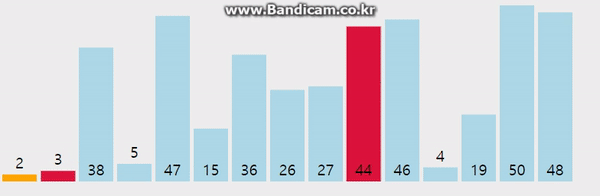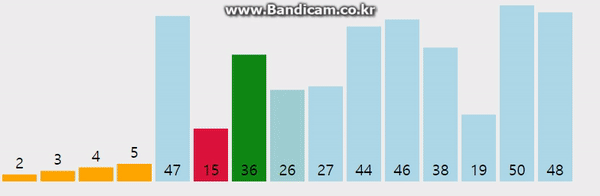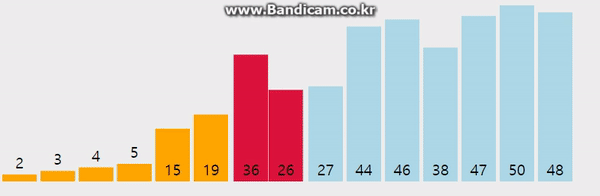
1-A. 어떻게 구현할까?
ex) 5, 4, 3, 2, 1
[풀이]
1. 5와 4를 비교하여 더 작은 값을 찾는다. → 4
2. 4와 3을 비교하여 더 작은 값을 찾는다. → 3
3. 3과 2를 비교하여 더 작은 값을 찾는다. → 2
4. 2와 1을 비교하여 더 작은 값을 찾는다. → 1
5. 최소값이 1이므로 맨 앞에 위치한 5와 교체(swap)한다. → 1, 4, 3, 2, 5
6. 위의 동작을 반복한다.
[규칙성]
- 로직의 반복수행 횟수는 n-1번
- 로직을 1회 반복할 때마다 비교를 위한 타겟 인덱스가 +1만큼씩 증가한다.
[규칙성을 코드로 구현]
for stand in range(len(data)-1):
lowest = stand
for index in range(stand+1, len(data)):
if data[lowest] > data[index]:
lowest = index
swap(data[stand], data[lowest])
1-B. 코드구현
def selection_sort(data):
for stand in range(len(data) - 1):
lowest = stand
for index in range(stand+1, len(data)):
if data[lowest] > data[index]:
lowest = index
data[stand], data[lowest] = data[lowest], data[stand]
return data
[테스트 및 결과]

2. 선택정렬의 시간복잡도
- 버블정렬과 동일하게 이중 for문에 의해 구현되는 코드이다.
- 그러므로 선택정렬의 시간복잡도는 O(n^2)이다.
- 상세하게 계산한다면 {n(n-1)}/2의 시간복잡도를 갖는다.
'컴퓨터공학기초 개념 > 알고리즘 개념' 카테고리의 다른 글
| Algorithm - 공간복잡도(Space Complexity) (0) | 2020.09.11 |
|---|---|
| Algorithm - 삽입 정렬(Insertion Sort) (0) | 2020.09.10 |
| Algorithm - 버블 정렬(Bubble Sort) (0) | 2020.09.09 |
| Data Structure - 개념 정리(summary) (0) | 2020.09.08 |
| Data Structure - Heap(2) (0) | 2020.09.03 |



댓글