0. 개요
- DFS와 BFS는 대표적인 그래프 탐색 알고리즘이다.
- DFS와 BFS가 어떻게 다른지, 언제 사용되는지 알아보자.
1. DFS(Depth First Search)
a) DFS의 탐색 방법
- DFS는 다음과 같은 탐색 순서를 갖는다.
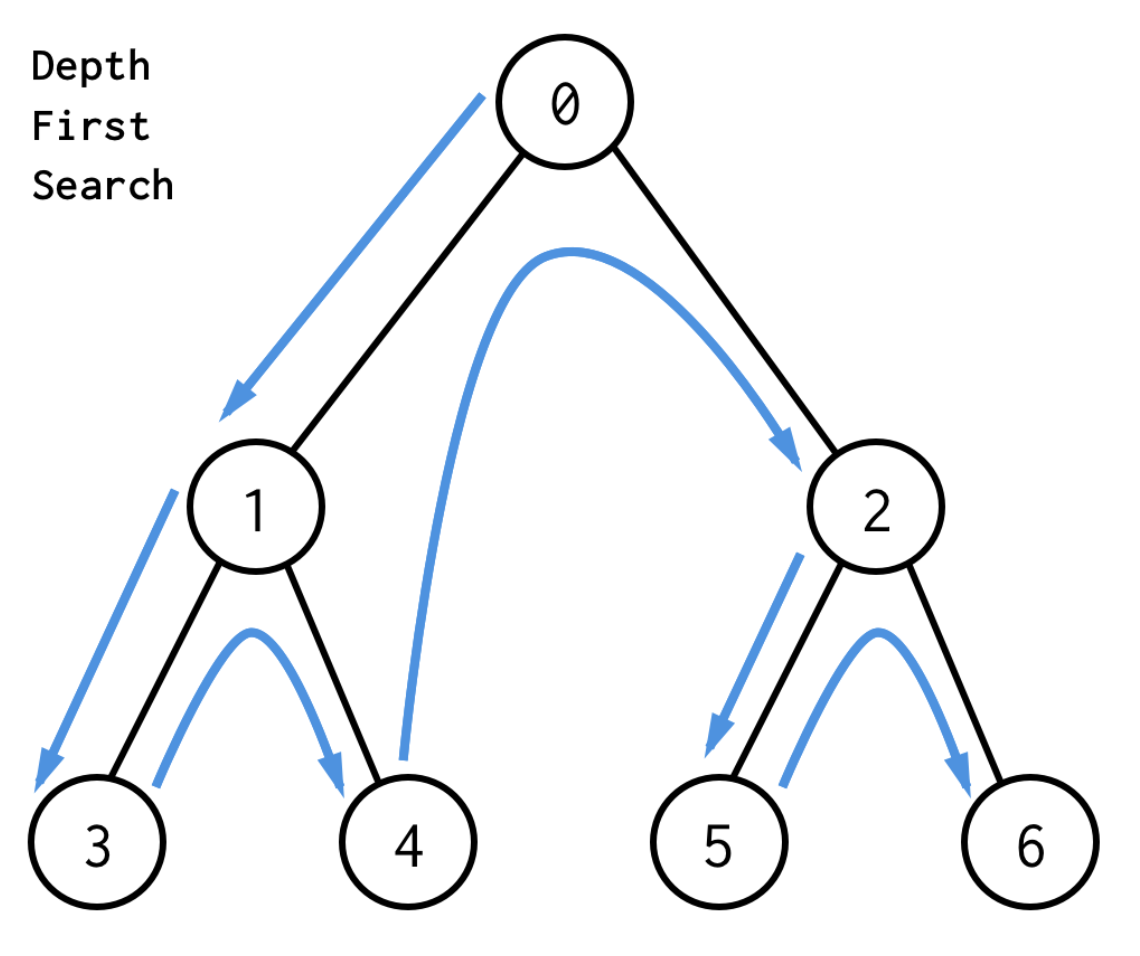
- DFS는 하나의 방향을 결정하면 그 방향을 따라 끝까지 도달한다.
▶ 트리의 경우, 왼쪽에 위치한 노드를 우선적으로 탐색한다.
▶ 그래프의 경우, 가중치 또는 특정 기준을 따라 탐색 방향의 우선순위를 결정한다.
- 위의 그림을 토대로 DFS는 다음과 같은 탐색 순서를 갖는다.
▶ 0번을 시작으로 왼쪽에 위치한 노드를 우선적으로 탐색한다. (0 ~ 3번 노드로 탐색)
▶ 3번 노드가 끝이므로 이전 단계로 돌아간다. (1번 노드로 돌아감)
▶ 1번 노드에서 오른쪽에 위치한 4번 노드를 탐색한다. (왼쪽을 다 탐색했기 때문에 오른쪽을 탐색)
- 여기까지 살펴보면 DFS의 탐색 순서와 비슷한 개념이 떠오르지 않는가?
- 한 가지 경우를 검증하고, 해당 경우가 틀린 경우라면 이전 단계로 돌아가는 방식 말이다.
- 그렇다. 재귀와 동일한 형태의 알고리즘을 갖는다.
b) DFS의 구현 - 재귀 함수
- 일반적으로 DFS는 재귀 함수로 구현된다.
- 트리 탐색에서 DFS 알고리즘은 다음과 같은 형태로 구현된다.
public class Tree {
public void dfs(Node root) {
if(root == null) return;
dfs(root.left);
dfs(root.right);
}
}
- 위의 코드의 로직은 간단하다.
- 왼쪽에 위치한 노드를 우선적으로 탐색한다.
- 해당 위치의 노드가 null이라면, 이전 케이스로 돌아온다.
- 오른쪽에 위치한 노드를 탐색한다.
- 이를 재귀적으로 반복한다.
c) DFS를 적용하는 경우
- 그렇다면 DFS는 언제 적용할까?
- DFS는 사이클(= 순환)의 존재 여부를 확인할 때 사용한다.
d) DFS가 사이클 확인에 사용되는 이유
- DFS가 사이클 여부를 확인할 때 사용되는 이유는 깊이를 우선적으로 탐색하기 때문이다.
- 즉, 하나의 방향이 잡히면 그 방향의 끝에 도달할 때까지 탐색하기 때문이다.
- 그러므로 사이클이 존재하는 방향만 찾으면 바로 사이클을 확인할 수 있다.
2. BFS(Breadth First Search)
a) BFS의 탐색 방법
- BFS는 다음과 같은 탐색 순서를 갖는다.

- BFS는 현재 위치를 기준으로 가장 가까운(= 인접한) 노드를 순차적으로 방문한다.
- DFS와는 다르게 끝까지 파고들지 않고, 주변을 순차적으로 확인하는 방식이다.
▶ 트리의 경우, 현재 위치의 좌/우 자식 노드를 순차적으로 탐색한다.
▶ 그래프의 경우, 가중치 또는 특정 기준에 따라 순차적으로 연결된 노드를 탐색한다.
- 위의 그림을 토대로 BFS는 다음과 같은 탐색 순서를 갖는다.
▶ 0번을 시작으로 좌/우측 자식 노드의 존재 여부를 확인한다.
▶ 좌측부터 1번 노드와 2번 노드를 순차적으로 방문한다.
▶ 1번 노드를 방문한다. 자식 노드인 3번, 4번 노드를 순차적으로 방문할 것을 기록한다.
▶ 2번 노드를 방문한다. 자식 노드인 5번, 6번 노드를 순차적으로 방문할 것을 기록한다.
▶ 3번, 4번, 5번, 6번 노드를 순차적으로 방문한다.
▶ 더 이상 방문해야 할 인접 노드가 없을 때까지 위의 과정을 반복한다.
- 여기까지 살펴보면 BFS의 탐색 순서와 비슷한 개념이 떠오르지 않는가?
- 다양한 경우를 순차적으로 방문하는 방식 말이다.
- 그렇다. FIFO(First in First out)와 동일한 형태를 갖는다.
b) BFS의 구현 - Queue 자료구조
- 일반적으로 BFS는 Queue 또는 FIFO 방식의 자료구조를 사용하여 구현된다.
- 트리 탐색에서 BFS 알고리즘은 다음과 같은 형태로 구현된다.
public class Tree {
static Queue<Node> que = new LinkedList<>();
public void bfs(Node root) {
if(root == null) return;
que.offer(root);
while(!que.isEmpty()) {
Node curn = que.poll();
if(curn.left != null) {
que.offer(curn.left);
}
if(curn.right != null) {
que.offer(curn.right);
}
}
}
}
- 위의 코드의 로직은 간단하다.
- 시작 노드(root)를 기준으로, 좌/우측의 자식 노드(= 인접 노드)를 확인한다.
- 좌/우측의 자식 노드가 존재한다면 순차적으로 방문하기 위해 Queue에 이를 저장한다.
- while 반복문을 사용하여 Queue에 저장된 인접 노드를 순차적으로 방문한다.
- Queue에 더 이상 방문할 인접 노드가 없을 때까지, 이를 반복한다.
c) BFS를 적용하는 경우
- 그렇다면 BFS는 언제 적용할까?
- BFS는 최단 거리/경로를 계산할 때 사용한다.
d) BFS가 최단 거리 계산에 사용되는 이유
- BFS가 최단 거리를 계산할 때 사용되는 이유는 인접 노드를 우선적으로 탐색하기 때문이다.
- 예를 들어, DFS는 목적지와 반대 방향을 탐색하더라도 끝까지 탐색을 수행한다.
- 그러므로 DFS는 최단 거리를 보장할 수 없다.
- 반면에, BFS는 인접 노드를 순차적으로 탐색한다.
- 이 방식으로 목적지와 가까운 노드를 순차적으로 탐색을 수행한다.
- 그러므로 BFS는 최단 거리를 확인하는데 유리한 알고리즘이다.
'Algorithm > 알고리즘 접근법 정리' 카테고리의 다른 글
| 최단거리 개념 및 문제 접근 방법 (0) | 2022.07.18 |
|---|---|
| DP(동적 계획법) 개념 및 문제 접근 방식 (0) | 2022.06.20 |
| 재귀 함수의 개념 및 문제 접근방식 (2) | 2022.03.11 |

댓글