1. 최단경로 알고리즘이란?
- 그래프에서 두 노드를 잇는 가장 짧은 경로를 찾는 알고리즘이다.
- 가중치 그래프(weighted graph)에서 간선(edge)의 가중치 합이 최소인 경로를 찾는 것이 목적이다.
2. 최단경로 문제의 종류
a) 단일 출발 및 단일 도착(Single-source & single-destination shortest path problem)
- 그래프 내의 특정 노드 A에서 출발하여 또 다른 특정 노드 B에 도착하는 가장 짧은 경로를 찾는 문제
b) 단일 출발(Single-source shortest path problem)
- 그래프 내의 특정 노드 A와 A를 제외한 그래프 내 모든 노드 각각의 가장 짧은 경로를 찾는 문제
c) 전체 쌍(all-pair) 최단경로
- 그래프 내의 모든 노드간 연결에 대한 최단경로를 찾는 문제
3. 최단경로 알고리즘 - 다익스트라 알고리즘
- 다익스트라 알고리즘은 최단경로 문제의 종류 중 b에 해당한다.
a) 다익스트라 알고리즘의 로직
- 첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단거리를 갱신하는 방법이다.
- 너비우선탐색(BFS)와 유사하다.
- 첫 정점부터 각 노드간의 거리를 저장하는 배열을 필요로 한다.
- 첫 정점의 인접 노드간의 거리(가중치)를 먼저 계산하고, 배열에 해당 노드의 거리를 업데이트 한다.
- 다익스트라 알고리즘 중 가장 개선된 알고리즘이 우선순위 Queue를 활용한 것이다.
b) 우선순위 Queue를 활용한 다익스트라 알고리즘
- 우선순위 큐는 MinHeap을 활용하여 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 된다.
1) 첫 정점(시작노드)을 기준으로 배열을 선언하여, 첫 정점에서 각 정점까지의 거리를 저장한다.
- 배열에는 초기에 첫 정점의 거리는 0(시작노드와 시작노드간의 거리), 나머지는 무한대(inf)로 저장한다.
- 우선순위 큐에는 (첫 정점=시작노드, 거리=0)을 삽입한다.
2) 우선순위 큐에서 노드를 꺼낸다.
- 처음에는 첫 정점(시작노드)만 저장되어 있기에, 첫 정점이 꺼내진다.
- 첫 정점과 인접한 노드를 대상으로, 첫 정점에서 각 인접노드와의 거리와 현재 배열에 저장되어 있는 각 노드와의 거리(inf)를 비교한다.
- 배열에 저장되어 있는 거리(inf)보다 첫 정점에서 각 인접노드와의 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다. (처음 배열에 저장되어 있는 거리는 0과 inf(무한대) 뿐이다.)
- 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에도 삽입한다.
- 결과적으로 너비우선탐색(BFS)과 유사한 방식으로, 첫 정점에 인접한 노드를 순차적으로 방문하게 되는 것이다.
- 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다 더 긴 거리를 가진 (노드,거리)의 쌍이 있는 경우에는 해당 노드와 인접한 노드간의 거리를 계산하지 않는다. - 위의 과정을 우선순위 큐에서 꺼낼 노드가 없을 때까지 반복한다.
4. 다익스트라 알고리즘의 이해
- 아래의 그래프를 기반으로 다익스트라 알고리즘 예제를 설명한다.
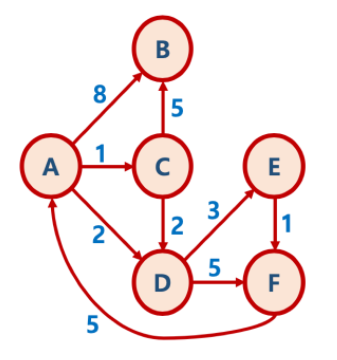
1단계 - 초기화
- 계산해야 하는 모든 경로는 A → B, A → C, A → D, A → E, A → F 이다.
- 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장한다.
- 처음에는 첫 정점의 거리를 0으로, 나머지 정점과의 거리를 inf(무한대)로 저장한다.
- 우선순위 큐에는 (첫 정점, 거리 0)만 먼저 저장한다.

2단계 - 우선순위 큐에 저장된 첫 정점과 거리(A, 0)를 꺼내와 인접노드와의 거리를 계산한다.
- 우선순위 큐의 경우, MinHeap을 사용하기 때문에 가장 짧은 거리의 정보를 가장 우선적으로 꺼낼 수 있도록 저장한다.
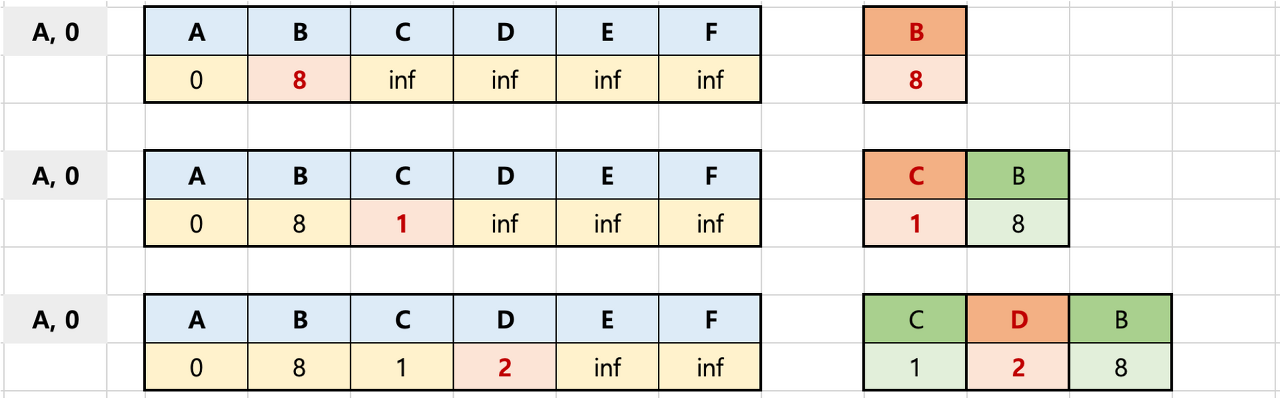
- 첫 정점인 A가 접근할 수 있는 인접노드와의 거리를 모두 계산하였다. 여기서 첫번째 싸이클이 종료된다.
- 2단계에서 계산된 경로는 A → B(8), A → C(1), A → D(2) 이다.
3단계 - 우선순위 큐에서 (C, 1)을 꺼내와 인접한 노드와의 거리를 계산한다.
- 우선순위 큐가 MinHeap이기 때문에 가장 짧은 거리를 갖고 있는 (C, 1)을 가장 먼저 꺼낸다(pop).
- 3단계에서 계산할 경로는 A에서 C를 거쳐가는 A → C → B, A → C → D 이다.

[3단계 해설]
- 기존의 A → B 경로는 8 이다. 하지만, C를 거쳐가는 A → C → B 경로의 거리는 6이다.
- A에서 B로 가기위한 경로가 A → B(8) 보다 A → C → B(6) 가 더 짧은 거리이므로 배열과 우선순위 큐를 업데이트 한다. - 기존의 A → D 경로는 2 이다. 그리고 C를 거쳐가는 A → C → D 경로의 거리는 3이다.
- A에서 C로 가기위한 경로가 A → C→ D(3) 보다 A → D(2) 가 더 짧은 거리이므로 업데이트 하지 않는다.
4단계 - 우선순위 큐에서 (D, 2)를 꺼내와 인접한 노드와의 거리를 계산한다.
- 4단계에서 계산할 경로는 A에서 D를 거쳐가는 A → D → E, A → D → F 이다. (화살표의 방향성때문에 다른 노드는 접근불가)

[4단계 해설]
- 기존의 A → E 경로는 inf(무한대)이고, A → D → E 경로의 거리는 5이다. (업데이트 수행)
- 기존의 A → F 경로는 inf(무한대)이고, A → D → F 경로의 거리는 7이다. (업데이트 수행)
5단계 - 우선순위 큐에서 (E, 5)를 꺼내와 인접한 노드와의 거리를 계산한다.
- 5단계에서 계산할 경로는 A에서 E를 거쳐가는 A → E → F 이다.

[5단계 해설]
- 기존의 A → F 경로는 7 이고, A → D → E → F 경로의 거리는 6이다. (업데이트 수행)
6단계 - 우선순위 큐에서 (B, 6)과 (F, 6)을 꺼내와 인접한 노드와의 거리를 계산한다.
- 6단계에서 계산할 경로는 A에서 B를 거쳐가는, A에서 F를 거쳐가는 A → B, A → D → F → A (F에서 A로 가는 경로가 존재하기 때문)이다.

[6단계 해설]
- A에서 B를 거쳐가는 경로는 A → B 밖에 존재하지 않는다. 그러므로 기존과 동일한 거리를 가지므로 업데이트 하지 않는다.
- A에서 F를 거쳐가는 경로는 A→ D→ F→ A 가 존재하며, 해당 경로의 거리는 11이므로 업데이트 하지 않는다.
7단계 - 우선순위 큐에서 (F, 7)과 (B, 8)을 꺼내와 인접한 노드와의 거리를 계산한다.
- A에서 F를 거져가는 경로와 A에서 B를 거쳐가는 경로의 최단경로가 이미 배열에 존재하므로 연산할 필요가 없다.
- 더 이상 우선순위 큐에 존재하는 데이터가 없기 때문에 알고리즘 연산을 종료한다.
5. 우선순위 큐의 장점
- 연산을 통해 지금까지 발견한 최단거리의 노드에 대해서 먼저 계산한다.
- 더 긴 거리로 계산된 경로에 대해서는 계산을 스킵할 수 있다. (끝까지 계산할 필요가 없다)
'컴퓨터공학기초 개념 > 알고리즘 개념' 카테고리의 다른 글
| Advanced Algorithm - MST(concepts of the MST)(1) (0) | 2020.09.29 |
|---|---|
| Advanced Algorithm - 최단경로(Shortest Path) 알고리즘(2) (0) | 2020.09.28 |
| Advanced Algorithm - 탐욕(Greedy) 알고리즘 (0) | 2020.09.26 |
| Advanced Algorithm - 깊이 우선 탐색(Depth First Search) (0) | 2020.09.25 |
| Advanced Algorithm - 너비 우선 탐색(Breadth First Search) (0) | 2020.09.24 |




댓글