1. 보수란 무엇인가?
- 컴퓨터는 1과 0으로 수를 표현한다.
- 컴퓨터는 오로지 덧셈만을 이용하여 연산을 처리한다.
- 이 과정에서 음수를 표현하거나, 음수 연산할 때 보수라는 개념을 사용한다.
- 이를 위해서 보수에는 여러가지 개념들과 기능이 있다. 같이 알아보자.
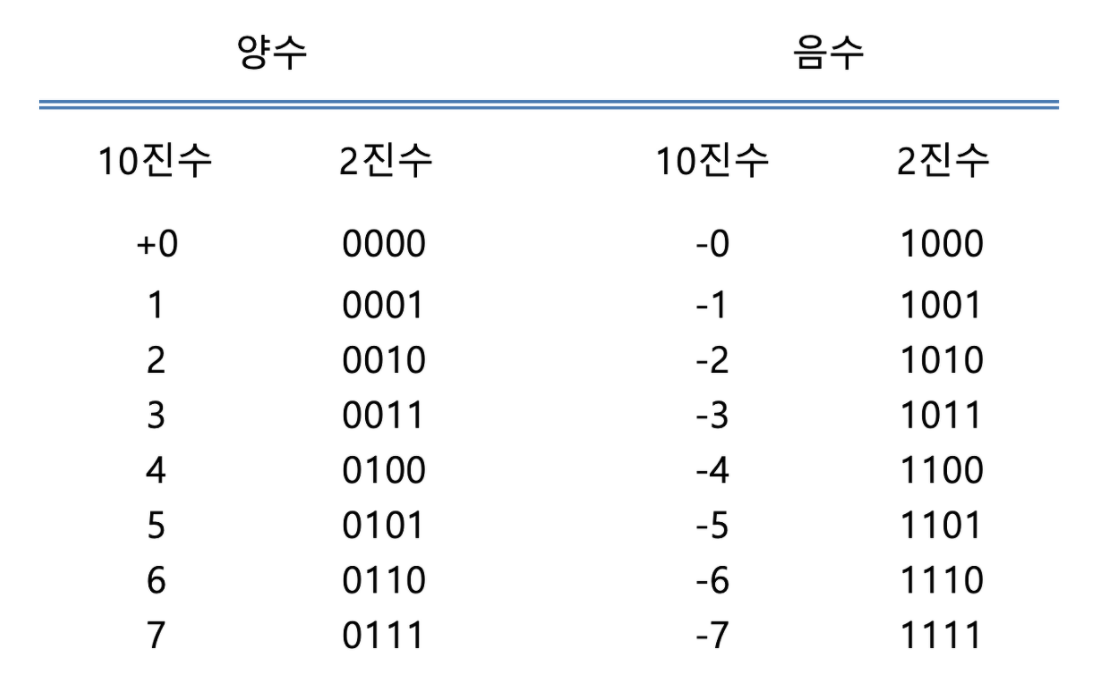
a) 부호 절대값(sign magnitude) - 음수를 표현하는 방법
- 2진법으로 수를 표현할 때, 가장 왼쪽의 값을 최상위 비트(MSB)라고 한다.
- 이 최상위 비트를 이용하여 음수를 표현해준다.
- 다음 예시를 통해 이해 해보자.
ex) 정수를 음수로 표현할때
- 정수(= int 자료형)는 보통 32bit(4byte)의 크기를 갖는다.
- 예를 들어, 5를 2진법으로 표현하면 다음과 같다.
ex) 5 = 0000 0000 0000 0000 0000 0000 0000 0101
- 이때 -5를 표현하려면 최상위 비트를 이용하여 다음과 같이 표현할 수 있다.
ex) -5 = 1000 0000 0000 0000 0000 0000 0000 0101
- 이 최상위 비트를 MSB(Most Significant Bit)라고 부른다.
b) 보수를 사용한 음수 연산 - 음수를 계산하는 방법
- 2진법으로 표현된 양수와 양수의 덧셈은 다음과 같다

- 최상위 비트가 동일한 경우에는 위의 연산처럼 어려울 것이 없다.
- 그러므로 음수간의 연산또한 동일하다.

- 그러나 문제점은 최상위 비트가 다른 경우에 발생한다.
- 다음 예시를 살펴보자.

- 위와 같은 경우에는 덧셈인가? 아니면 뺄셈인가?
- 가장 간단한 해결책은 절대값이 큰 수를 앞으로 보내주는 것이다.
- 그리고 절대값 상태에서 연산을 한다.
- 두 수 중 하나라도 최상위 비트가 음수를 표현한다면 절대값 간의 뺄셈을 수행한다.
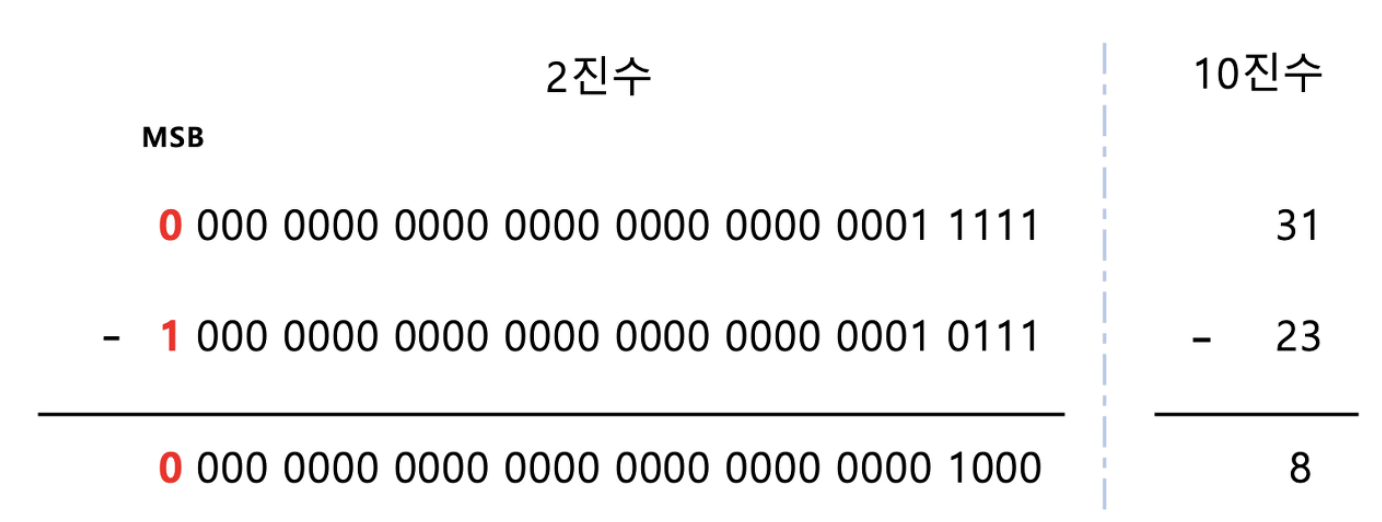
- 절대값이 더 큰 값을 앞으로 보내고 난 후에 계산을 한다.
- 계산 후 절대값이 더 큰 값의 최상위 비트를 계산된 값에 적용한다.
- 만약 절대값이 더 큰 값이 음수인 경우에는 어떨까?
- 다음 예시를 살펴보자.

- 마찬가지로 절대값이 큰 값을 앞으로 보낸다.
- 둘 중 하나라도 최상위 비트가 존재한다면 절대값 간의 뺄셈을 진행한다.
- 그리고 절대값이 더 큰 수의 최상위 비트를 계산된 값에 적용한다.
c) 컴퓨터에는 뺄셈이 없는데?
- 이 포스팅의 맨 첫 부분에서 분명히 컴퓨터는 덧셈만을 사용 한다고 했다.
- 그러나 위의 연산 예시를 살펴보면, 뺄셈을 사용한 것을 확인할 수 있다.
- 분명히 덧셈밖에 할 줄 모르는 컴퓨터인데 어떻게 뺄셈을 한걸까?
▶ 컴퓨터는 음수를 처리하기위해 보수라는 개념을 사용한다.
▶ 즉, 보수를 사용하여 뺄셈을 덧셈으로 처리하는 것이다.
▶ 어떻게 그게 가능한가?
▶ 이를 이해하기 위해서는 다음의 개념을 알아야 한다.
2. 보수를 통해 뺄셈을 덧셈으로 처리하는 방법
a) 어떤 수의 보수를 구하는 방법
- 어떤 수의 보수라는 것은 무엇인가?
- 어떤 수를 만들기 위해서 보충되어야 하는 수를 의미한다.
- 이게 도대체 무슨 뜻인가? 다음 예시를 살펴보자.

- 10진수로 간단한 예시를 살펴보자.
- 9에서 6을 빼면 3이라는 값이 나온다. 하지만, 컴퓨터는 뺄샘을 할 수 없다.

- 그렇다면 9에 어떤 수를 더해서 3이 나오도록 해야한다.
- 이러한 상황을 "-6에 대한 보수를 구한다" 라고 말한다.
- 10진법을 사용하고 있으니 "-6에 대한 10의 보수를 구한다" 라고 말한다.
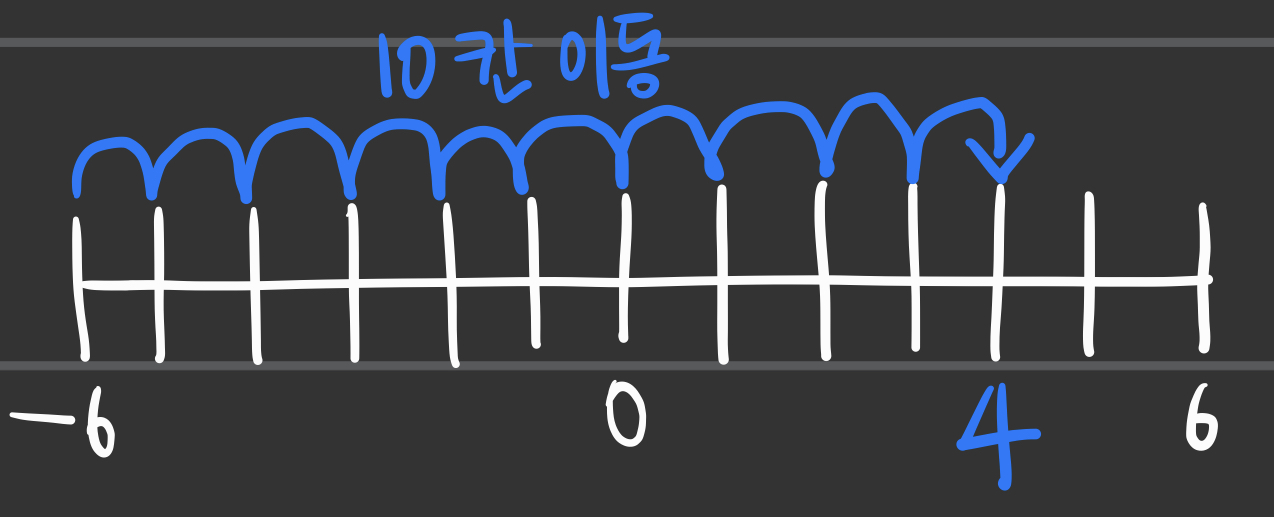
- 보수를 구하는 법은 굉장히 간단하다.
- 10진법을 사용하고 있으니 -6부터 10칸 이동하면 되는 것이다.

- 그러면 이렇게 4라는 값이 나온다.
- 4는 -6에 대한 10의 보수가 되는 것이다.

- 그렇다면 아까의 예시로 돌아가보자.
- 9에 4를 더했더니 13이 나온다.
- 3이 아니라 13이 나오는데 어떻게 해야 하는가?
- 컴퓨터는 여기서 10의 자리를 날려버리고 1의자리인 3만 사용한다.
- 이것이 보수를 구하는 방법이며, 뺄셈을 덧셈으로 계산하는 방법이다.
연습) 10의 보수를 구해보자.
1. 13-10 = 3일 때, -10에 대한 1의 보수를 구해보자.
▶ -10에 대한 10의 보수는 -10 + 10 = 0
▶ 13 + 0 = 3
▶ 그러므로, -10에대한 10의 보수는 0이 된다.
- 여기까지 10진법을 이용해서 보수를 구하는 방법과, 뺄셈을 덧셈으로 처리하는 방법을 알아보았다.
- 그러면 2진법에서는 어떻게 할까? 다음 포스팅에서 같이 알아보자.
[자료출처]
'컴퓨터공학기초 개념 > 컴퓨터구조' 카테고리의 다른 글
| 6. 데이터 표현 - 2의 보수를 사용하는 이유 (3) | 2021.08.03 |
|---|---|
| 5. 데이터 표현 - 2의 보수 (Two's complement) (0) | 2021.08.03 |
| 4. 데이터 표현 - 1의 보수(one's complement) (0) | 2021.08.03 |
| 2. 데이터의 표현 - 진법 (0) | 2021.08.02 |
| 1. 컴퓨터의 구성요소 및 기능 (0) | 2021.08.02 |




댓글