0. 시작하기전에
- 한동안 알고리즘 공부를 하며 깨달은게 있다.
- 알고리즘을 얼마나 외우고 있느냐는 코딩테스트에서는 중요하지 않다는 점이다.
- 결국 이론적인 이해도와 지식에 대한 소화시간을 충분히 갖고, 이를 기반으로 응용적인 사고가 가능하냐는 부분이 가장 중요하다.
- 그러므로 코드를 외우려 노력하지말고, 그 안의 규칙성과 논리를 이해하기 위해 더 시간을 투자하기를 바란다.
1. String Match
- 문자열을 탐색하는 방법론이다.
- 대표적으로 KMP 알고리즘과 Rolling Hash를 사용하여 구현한 Rabin Karp 알고리즘이 있다.
- 일반적으로 String Match 알고리즘은 O(n)의 시간복잡도를 갖는다.
a) 시간복잡도
- 문자열 탐색은 다음과 같은 과정을 거친다.
string1 = ["abc", "abd", "abk"] # 원래는 "abcabdabk" 이다.
sub_string = "abk"- 위의 예시처럼 string1에서 sub_string과 동일한 부분이 있는지를 찾게된다.
- string1에서 sub_string을 찾기 위해서는 문자열의 각 문자를 탐색하면서 동일한 문자열의 index를 찾게된다.
- string1의 길이가 n이고 sub_string의 길이가 m일 때, 해당 sub_string을 찾는데 걸리는 시간복잡도는 O(n)이 된다.
2. KMP 알고리즘
- string과 sub_string 각각에 포인터를 생성하여 각 문자를 비교하는 알고리즘이다.
- 다음 예시를 통해 이해해보자.
a) 2개의 포인터를 만들어 글자를 비교한다.
- 각 문자열마다 포인터를 생성하여 각 문자를 비교한다.
- 글자가 같은 경우, 2개의 포인터 모두 한칸씩 이동한다.
- 글자가 다른 경우, string의 포인터를 한칸 이동한다.

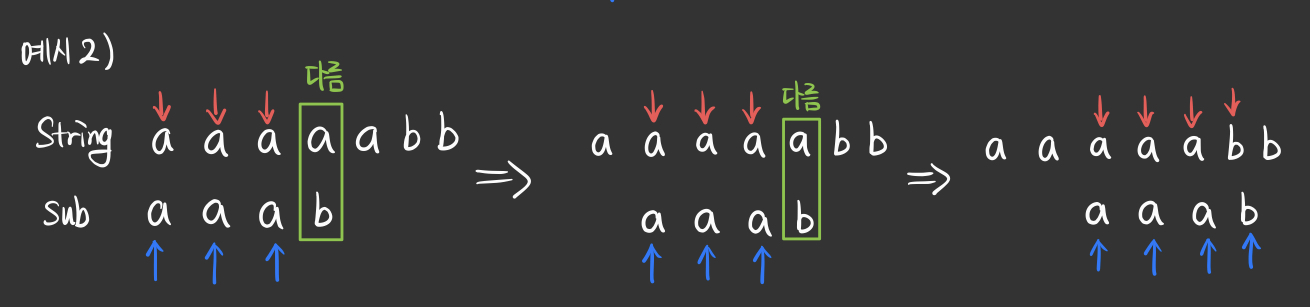
- 예시 2번의 경우, O(n * m)의 시간복잡도를 갖는다. sub_string에서 a가 반복되는 구간이 있기 때문이다.
- 즉, String의 포인터를 한칸 이동할 때마다, sub_string의 길이만큼 비교연산은 하게 되는 것이다.
- 그러면 이 문제는 어떻게 해결할 수 있을까?
- 간단하다. 반복되는 부분보다 반복되지 않는 부분을 우선적으로 탐색하면 된다.
- 이러한 이유로 KMP 알고리즘이 발명되었다.
b) 반복되는 패턴을 찾는 방법
- sub_string을 구성하는 문자의 반복횟수를 확인하여 패턴을 확인하는 방법을 사용한다.
- 다음과 예시를 살펴보자.

c) 예시1 - 패턴을 이용한 문자열 Matching




c) 예시2 - 패턴을 이용한 문자열 Matching
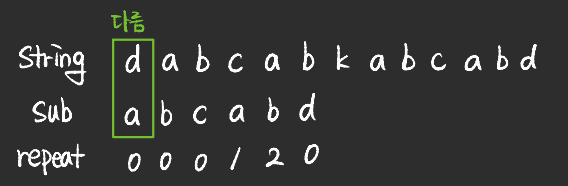



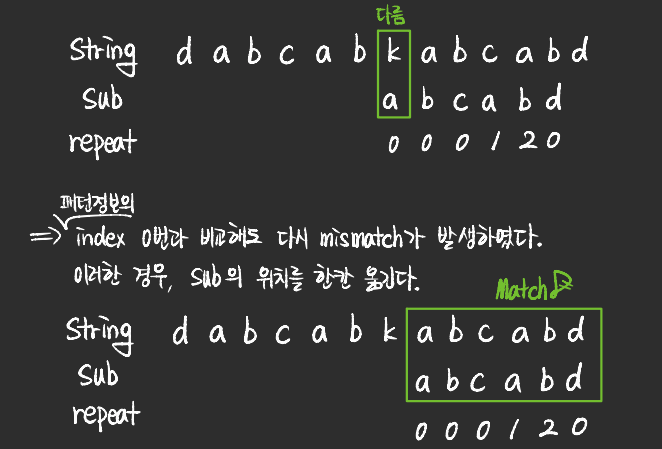
- 이처럼, 최종적으로 matching 되는 문자열을 찾게 된다.
- 반복되는 문자열에 대한 패턴정보를 기반으로 matching 문자열을 찾는 방식을 KMP 알고리즘이라고 한다.
- 반복되는 문자열에 대한 탐색을 하지 않으므로, KMP 알고리즘은 O(n)의 시간복잡도를 갖는다.
3. Rabin Karp 알고리즘(feat. Rolling Hash)
* Rolling Hash라는 이름처럼, 기본적으로 Hash 또는 Hash 테이블에 대한 이해를 필요로 한다.

- 우선 sub_string의 길이(5)와 hash 값(42)을 구한다.
- sub_string의 길이만큼 string의 문자들을 묶어서 hash 값을 구한다.
- 즉, sub_string의 hash 값과 동일한 hash 값을 가진 string의 문자열을 찾는 방식이다.
a) window sliding을 통한 탐색


b) 예시2

- 이처럼 sub_string의 길이만큼 string을 나누고, 나누어진 문자열의 hash값과 sub_string의 hash값을 비교한다.
- 동일한 hash 값을 가진 문자열을 찾는다면, 각 문자를 비교하여 한번 더 확인한다.
- 단순히 hash값을 이용하여 문자열을 탐색하는 것으로, O(n)의 시간복잡도를 갖는다.
- 이와 같은 방식이 Rolling hash를 이용한 Rabin Karp 알고리즘이다.
* 만약 면접이나 코딩테스트에서 String Match문제가 나온다면, KMP보다 Hash를 이용한 Rabin Karp 알고리즘을 추천한다.
3. Palindrome

'Algorithm > 알고리즘 공부노트' 카테고리의 다른 글
| Return에 대하여 (0) | 2021.11.28 |
|---|---|
| 파이썬 클래스와 self의 의미 (1) | 2021.11.06 |
| 11. Array(배열) - Radix Sort (0) | 2021.10.08 |
| 10. Array(배열) - Counting Sort (0) | 2021.10.05 |
| 9. Array(배열) - Heap Sort(2) (0) | 2021.09.09 |



댓글