0. 시작하기 전에
- 지금까지 배운 알고리즘은 O(n^2) 또는 O(n log n)의 시간복잡도를 갖는다.
▶ O(n^2): bubble, insertion
▶ O(n log n): merge, quick
- Counting Sort는 O(n + k)의 시간복잡도를 가진다.
- Counting Sort를 이해하며 k의 의미가 무엇인지 알아보자.
1. Counting Sort(계수정렬)
- Counting Sort는 주어진 array의 요소를 counting하여 정렬하는 알고리즘이다.
a) Counting Sort의 정렬과정







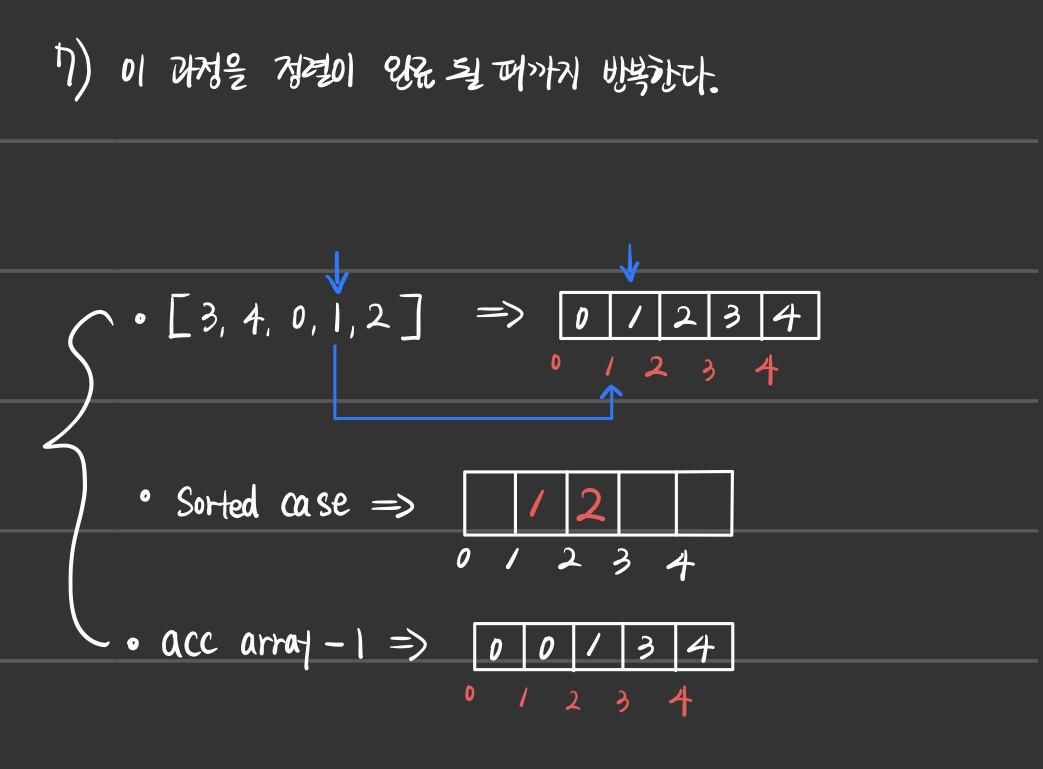


2. 코드 구현
- 위에서 진행한 과정을 코드로 그대로 구현하면 Counting Sort 알고리즘이 완성된다.
- 다음 코드를 확인해보자.
from typing import List
def countingSort(nums:List[int])->List[int]:
length = len(nums)
min_num = min(nums) # 가장 작은 수
max_num = max(nums) # 가장 큰 수
range = max_num - min_num + 1 # count array를 만들기 위한 크기 설정
count_array = [0] * range # count array 생성
for num in nums: # count array의 요소를 채우는 과정
count_idx = num - min_num # min_num이 0이 아닌 경우, index 0번이 비어있게 되기 때문에 이를 방지하기 위함.
count_array[count_idx] += 1
acc_counts = [] # acc(누적) array 생성
acc_count = 0 # acc array의 요소가 될 값
for count in count_array: # acc array의 요소를 채우는 과정
acc_count += count
acc_counts.append(acc_count)
end_locs = [ c-1 for c in acc_counts] # acc array - 1 배열을 만드는 과정
sorted = [0] * length # 최종적으로 정렬될 배열 생성
for num in reversed(nums): # 맨 뒤의 요소부터 정렬을 시작하는데, 이를 리버스로 구현
count_idx = num - min_num
end_loc = end_locs[count_idx]
sorted[end_loc] = num
end_locs[count_idx] -= 1
return sorted3. K의 의미
- 앞에서 Counting Sort는 O(n + k)의 시간복잡도를 갖는다고 했다.
- 여기서 K는 주어진 배열의 가장 큰 요소의 값을 의미한다.
- 더욱 자세히 말하자면, 주어진 배열의 가장 큰 요소와 가장 작은 요소의 차이를 의미한다.
a) K의 중요성
- 주어진 배열의 가장 큰 요소와 작은 요소의 차이가 왜 Counting Sort의 시간복잡도에 영향을 주는 것일까?
- 그 이유는 count_array를 만드는 과정에 있다.
- 예시로 [0, 1, 900] 이렇게 3가지 요소를 갖는 배열을 counting sort를 이용하여 정렬한다고 가정해보자.
- count_array를 만들기 위해서, count_array의 길이를 (max_num - min_num + 1)을 통해서 계산한다.
- 그렇다면, 위의 배열을 사용했을 때 count_array의 길이는 (900 - 0 + 1)을 통해서 901이 되는 것이다.
- 요소 3개짜리 배열을 정렬하기 위해서 901개의 자리를 갖는 count_array를 사용하게 된다.
- 그러므로 count_array를 이용한 acc_array를 만들기 위해서 for문을 돌리는 과정과,
- acc_array를 이용하여 end_locs를 만들기 위해 for문을 돌리는 과정에서 각각 901번의 연산을 수행해야 하는 것이다.
- 즉, K는 주어진 배열의 가장 큰 수와 가장 작은 수의 차이를 의미하며
- 이와 같은 이유로, K가 Counting Sort의 시간복잡도에 영향을 끼치는 것이다.
ex) K가 100인, 10개의 요소(n)를 가진 배열을 Counting Sort로 정렬하는 경우
→ 여기서 k = n ^ 2 이므로, 해당 배열을 정렬하는데 O(n^2)의 시간복잡도를 갖는다.
'Algorithm > 알고리즘 공부노트' 카테고리의 다른 글
| 12. String Match(KPM, Rabin-Karp, Palindrome) (0) | 2021.10.20 |
|---|---|
| 11. Array(배열) - Radix Sort (0) | 2021.10.08 |
| 9. Array(배열) - Heap Sort(2) (0) | 2021.09.09 |
| 8. Array(배열) - Heap Sort(1) (0) | 2021.09.09 |
| 7. Array(배열) - Quick Sort(퀵 정렬) (0) | 2021.09.06 |




댓글