1. 실무 적용 사례
- 우선 실무 적용 사례를 통해서 부울대수와 진리표에 대해서 간략하게 알아보자.

- 단일 비트(한자리 비트) 연산을 할 때 S는 a + b 값을 담는다.
- C는 Carry라고 부르며 1 + 1를 연산하면 발생하는 초과값을 담는다.
- 진리표는 단일 비트 계산의 모든 경우의 수를 적은 표를 말한다.

- 부울대수는 S 값에 대한 관계를 표현한 식이다.
- 부울대수를 확인하면 배타적 논리합이라는 것을 알 수 있는데, 이는 S값을 보면 된다.
- 0 + 0 일 때 0이고 1 + 0 또는 0 + 1일 때 1이 나오는 배타적 논리합 관계인 것을 알 수 있다.
- C계산 과정도 논리 곱의 형태라는 것을 알 수 있다.
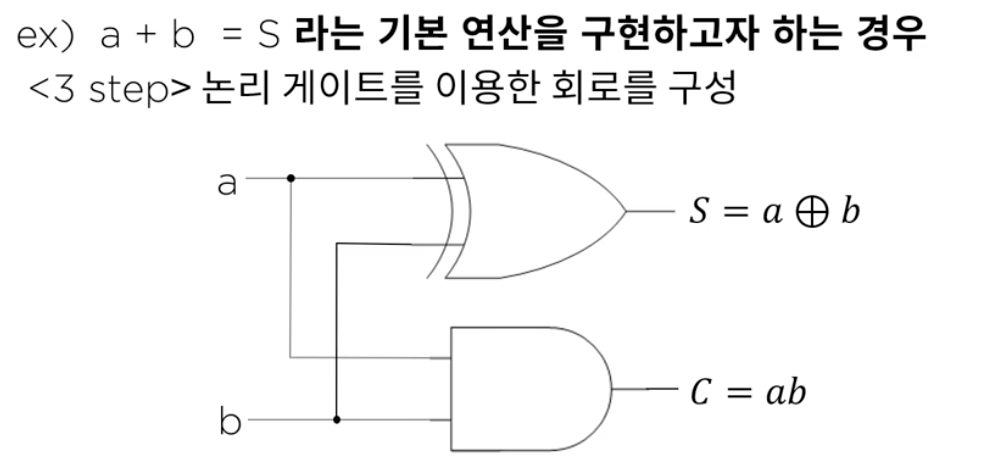
- 이를 기반으로, 단일비트 합에 대한 연산을 논리 회로로 구성을 하면 위와 같이 나온다.
- 감이 오는가? 그렇다면 더 자세히 알아보자.
2. 부울대수(Boolean Algebra)란?
- Boolean Algebra를 해석하면 논리 연산이라는 것을 알 수 있다.
- 즉, True와 False를 이용하여 논리적 명제를 수학적으로 표현한 것이다.
- 쉽게 말하자면, 집합의 개념과 동일하다. 집합으로 이해하자.
- 이는 1845년 영국의 수학자 G.Boole에 의해 정립된 개념이다.
a) 부울대수의 사용
- 부울대수는 다음과 같이 사용된다.
▶ 논리회로의 형태와 구조를 표현할 때
▶ 진리표의 관계를 수식으로 표현할 때
▶ 동일한 성능에 대해, 더 간단한 회로를 만들 때
3. 부울대수의 기본법칙
- 부울대수는 다음 4가지 법칙을 기반한다.
▶ 교환 법칙(commutative Law)
▶ 결합 법칙(Associate Law)
▶ 분배 법칙(Distributive Law)
▶ 드모르간의 정리(De Morgan's Law)
a) 교환법칙
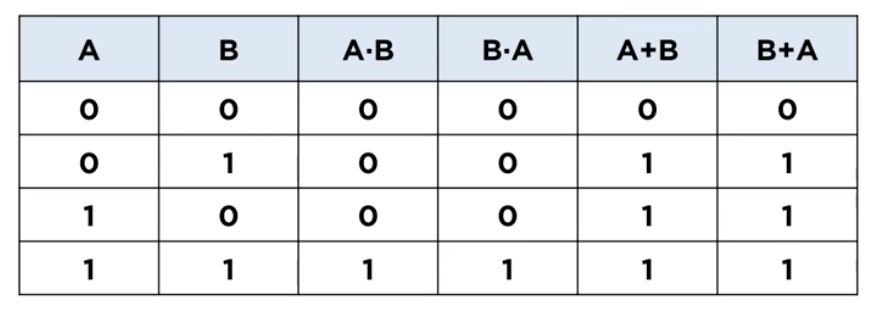
▶ A * B = B * A
▶ A + B = B + A
- 집합으로 표현하면 다음과 같다.

- 논리 회로로 표현하면 다음과 같다.

b) 결합법칙
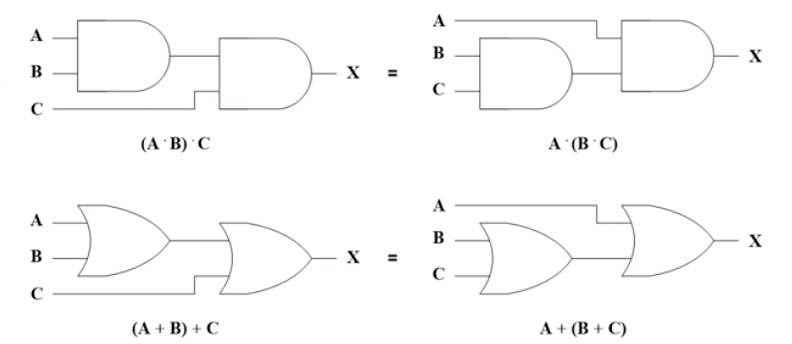
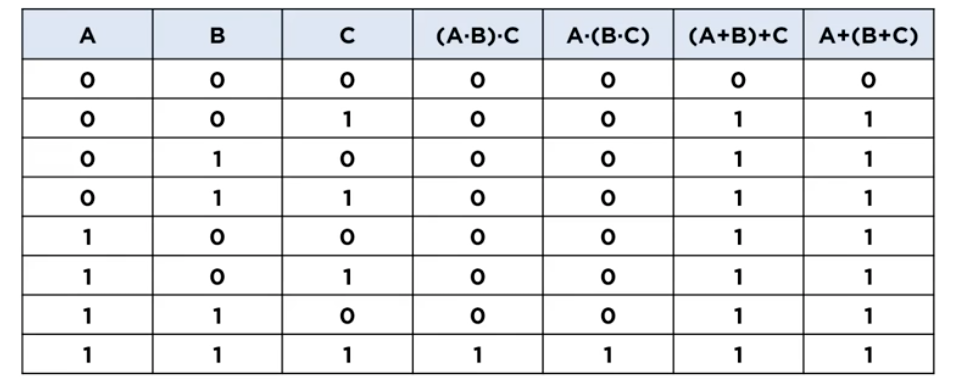
▶ A * (B * C) = (A * B) * C
▶ (A + B) + C = A + (B + C)
- 집합으로 표현하면 다음과 같다.

- 논리 회로로 표현하면 다음과 같다.
c) 분배법칙
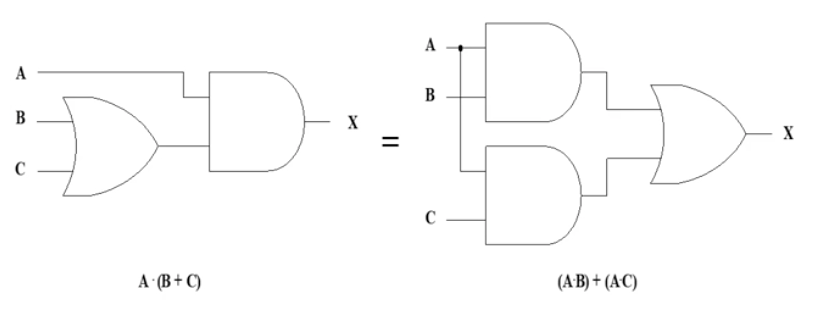
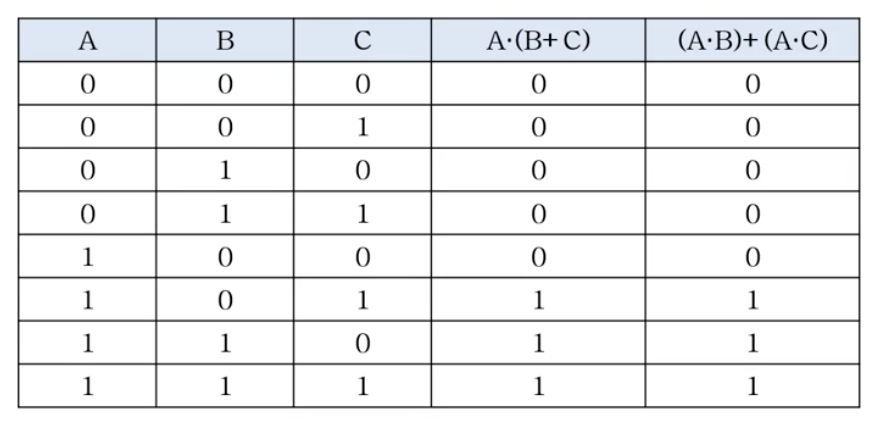
▶ A * (B + C) = AB + AC
- 집합으로 표현하면 다음과 같다.

- 논리 회로로 표현하면 다음과 같다.
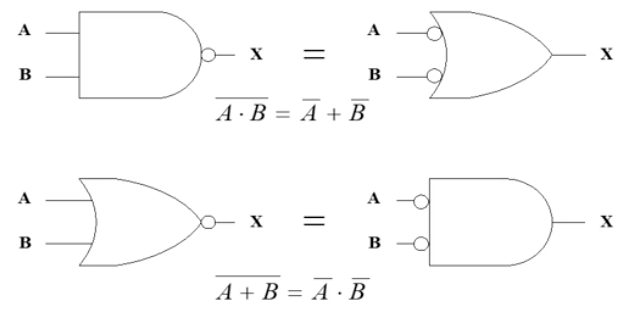
d) 드모르간의 법칙
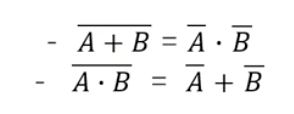
- 저 머리위의 작대기는 NOT을 의미한다. 즉, 여집합이다.
- 다른 말로 보수를 취한다고 한다.
- A가 1이면 A 바는 0이 된다.
- 집합으로 표현하면 다음과 같다.
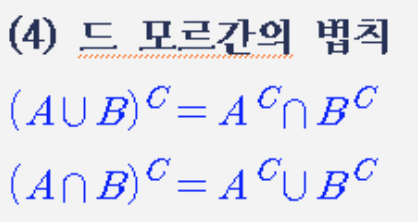
- 논리 회로로 표현하면 다음과 같다.
3. 부울대수를 이용한 논리식의 간편화
- 다음의 식을 간편화 / 간략화 해보자.
E = (a' + bc)(a + b)
- 분배 법칙으로 통해 식을 전개해보자.
E = aa' + a'b + abc + bbc- aa' 는 0이 되므로 생략이 가능하다.
- aa' 가 0이 되는 이유는 a가 1인 경우 a'는 0이고 ark 0인 경우 a'는 1이기 때문이다.
- 그러므로 aa'의 논리곱은 0이 나올 수 밖에 없다.
E = a'b + abc + bc- bbc가 bc로 바뀌었다.
- b가 1인 경우 b*b = 1이 된다.
- b가 0인 경우 b*b = 0이 된다.
- 그러므로 b*b = b와 동일하다.
E = (a + 1)bc + a'b- 결합법칙을 이용하여 공통부를 묶어준다.
E = bc + a'b- (a + 1) 부분이 생략되었다. 그 이유는 다음과 같다.
- a가 1인 경우, (a + 1) = 1 + 1이 된다. 즉, 1이다.
- a가 0인 경우, (a + 1) = 0 + 1이 된다. 즉, 1이다.
- 그러므로 (a + 1) * bc 는 1 * bc와 동일하기 때문에 생략된다.
E = (a' + bc)(a + b)
E = bc + a'b- 최종적으로 다음과 같이 간략화 되었다.
- 간략화를 하게 되면 논리 회로를 설계할 때, 더 짧은(= 간단한) 회로를 구성할 수 있다.
'컴퓨터공학기초 개념 > 컴퓨터구조' 카테고리의 다른 글
| 12. 논리회로 - 조합논리회로 (0) | 2021.08.06 |
|---|---|
| 11. 논리회로 - 카르노맵(karnaugh map) (0) | 2021.08.06 |
| 9. 논리회로 - 논리 게이트(logical gate) (1) | 2021.08.05 |
| 8. 데이터 표현 - BCD, 패리티 비트, 해밍코드 (0) | 2021.08.05 |
| 7. 데이터 표현 - 실수 (1) | 2021.08.04 |




댓글