1. 카르노 맵을 사용하는 이유
- 이전 포스팅에서 부울 대수를 이용하여 진리표를 도출해냈고 그것을 활용하여 논리식을 구하는 법을 배웠다.
- 부울 대수를 이용해 논리식을 구할 수는 있으나, 여러가지 규칙을 따라야 하는 불편이 있었다.
- 카르노 맵은 부울 대수보다 빠르게 진리표를 만들 수 있는 방법으로,
- 이를 이용하여 논리식을 간소화 할 수 있고 빠르게 계산할 수 있다.
- 이와 같은 이유로 카르노 맵을 사용한다.
2. 카르노 맵 - 기본개념
a) map이란?
- map이란, 변수의 개수에 따라 작성되는 표를 의미한다.
b) 민텀(minterm)이란?
- 곱들의 합을 말하는 것으로, map의 사각형 하나를 minterm 이라고 부른다.
- 최소항을 의미하는 것으로, map의 최대항(합들의 곱)을 maxterm 이라고 부른다.
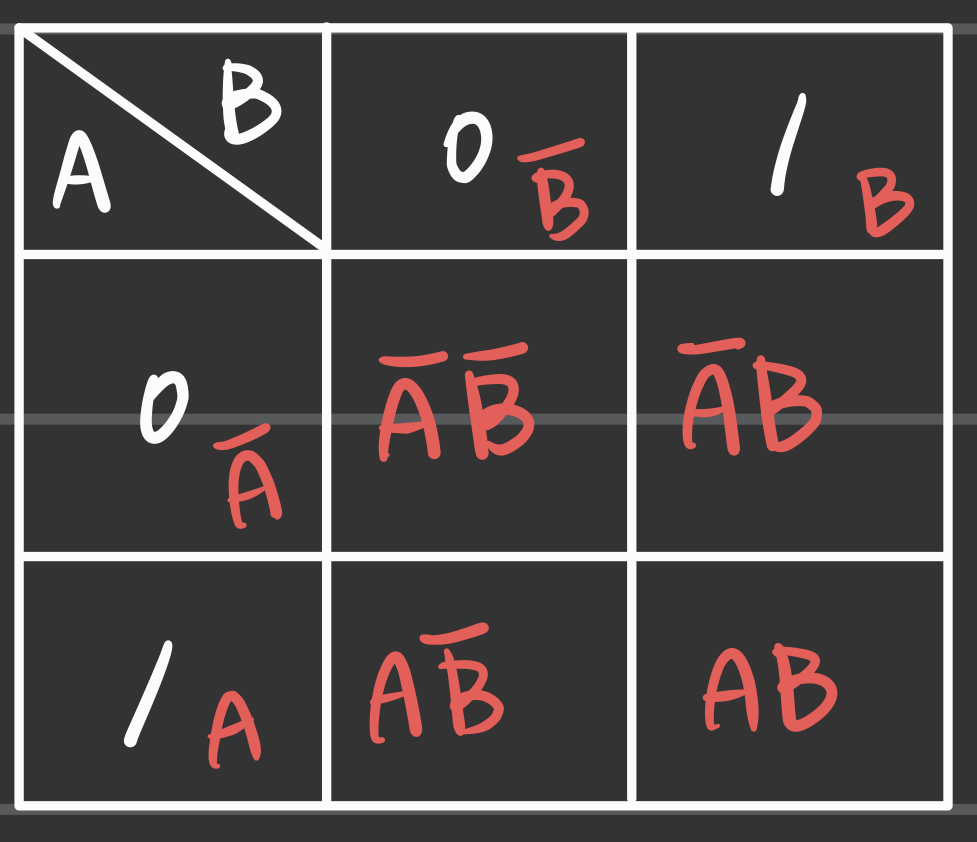
b) 0인 부분이 각 변수의 NOT이 된다.
- 집합에서 집합 이름 위에 짝대기를 그으면 NOT을 표현한다.
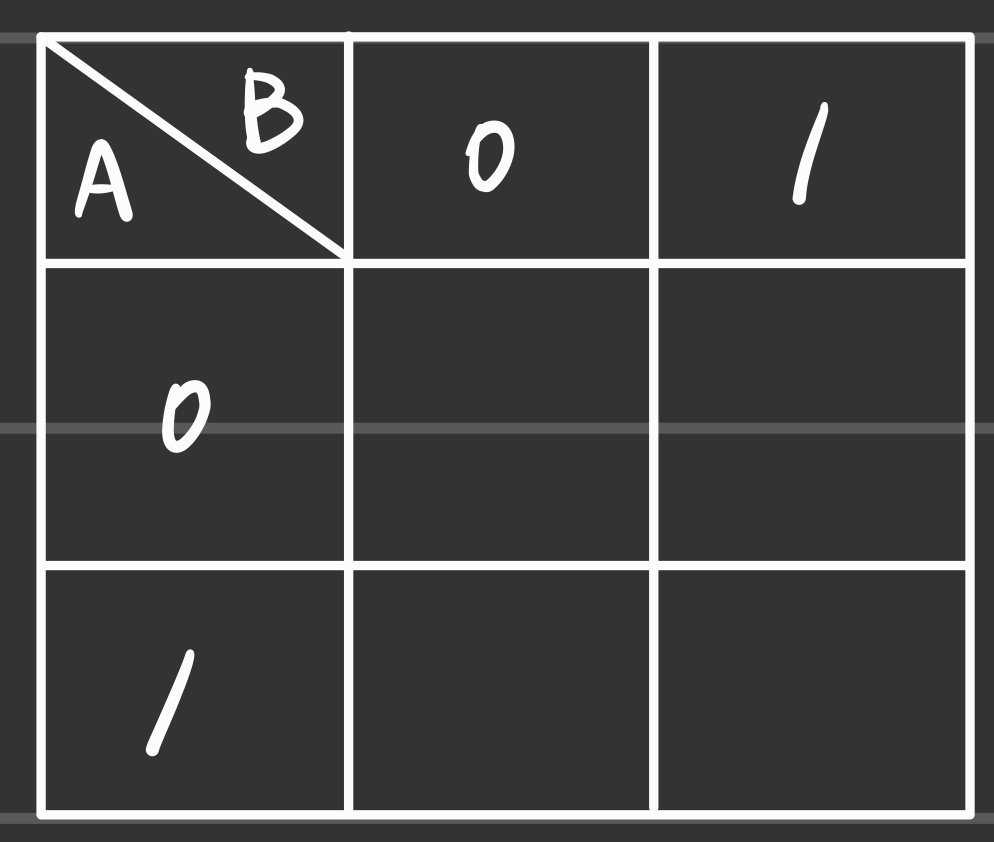
- 아래의 map은 변수가 2개일 때의 map인데, 다음과 같이 생각하면 된다.
c) 카르노 맵은 순환한다.
- 카르노 맵은 변수가 순차적으로 증가하지 않는다.
- 아래의 그림에서와 같이 0, 1, 3, 2로 나열된다.
- 그 이유는 비트가 1 단위씩 변하기 때문이다. 0에서 1로 1에서 0으로 말이다.
- 그렇기 때문에 다음과 같은 불규칙적인 수열이 생성된다.
- 그러나 이로 인해 수열의 순환이 생성된다.

d) 인접된 변수끼리 묶을 수 있다.
- 카르노 맵은 인접된 변수끼리 묶을 수 있다.
- 몇가지 예시를 보자.
예시1)
- 일반적인 묶음의 형식이다.
- 수평, 수직 등 어떤 형태로든 인접한 변수끼리 묶일 수 있다.

예시2)
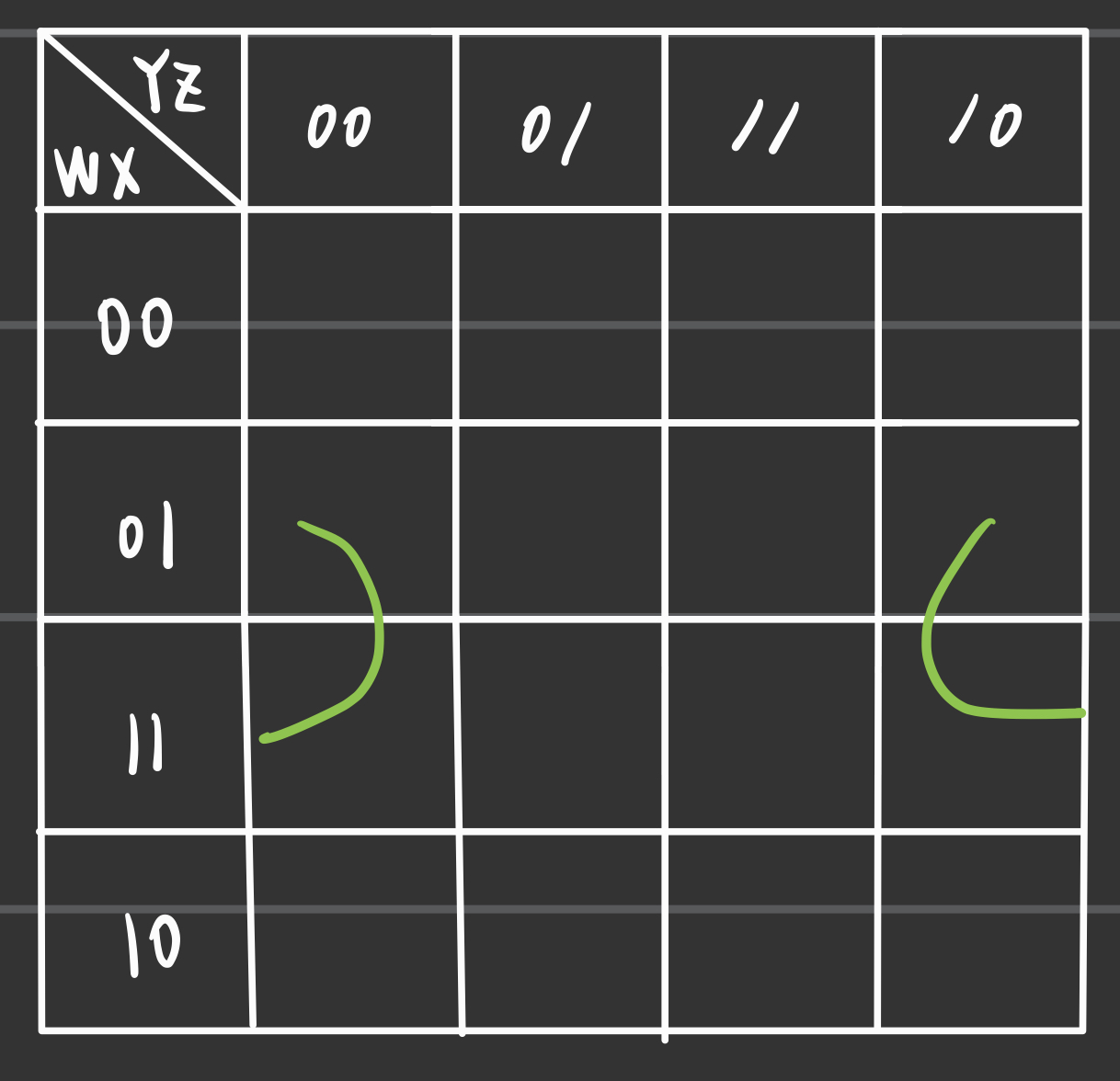
- 귀퉁이 끼리 묶인 모습이다.
- 이는 카르노 맵이 순환한다는 특성으로 인해 가능한 것이다.
- 모서리가 서로 인접한다고 생각하면 이해하기 편하다.
예시3)
- 예시2와 마찬가지로 모서리 모두 서로 인접한다.
- 마치 만두처럼, 모퉁이가 접혀 서로 인접한다고 생각하면 편하다.

3. 카르노 맵 - 문제풀이
- 시작하기에 앞서서, 모든 연산을 집합이라고 생각하고 이해하기를 바란다.
- 집합으로 생각하고 이해하면 연산이 쉽게 이해될 것이다.
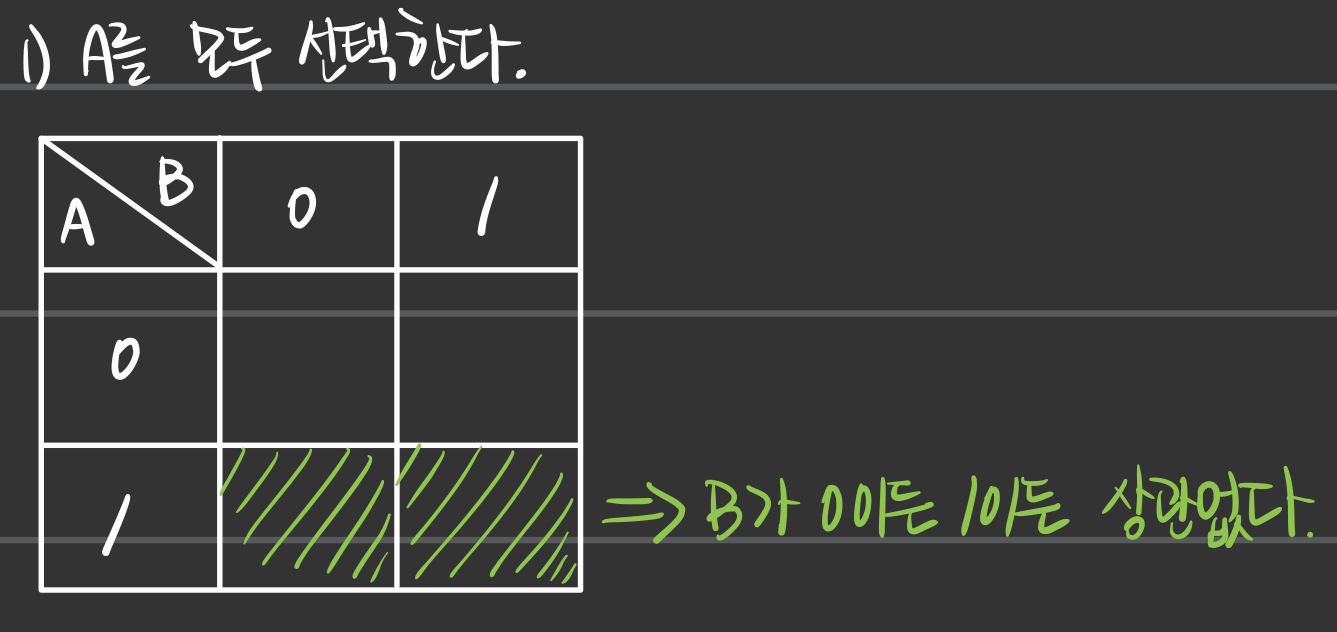
a) A + A·B 를 구하라


b) A · (A+B) 를 구하라

c) ABC' + AB'C' + A'BC' + A'B'C' 를 구하라

- Don't care 라는 개념이 등장한다.
- Don't care 라는 개념은 1과 0 모두 해당되는 경우를 의미한다.
- Don't care 조건에 해당한다면 생략하면 된다.
d)WXYZ' + WXY'Z' + W'XYZ' + W'XY'Z' 을 구하라
- 이제 어느정도 익숙해졌으니 쉽게 푸는 방법을 이용해보자.

- 여기까지 카르노 맵에 대해서 알아보았다.
[자료출처]
'컴퓨터공학기초 개념 > 컴퓨터구조' 카테고리의 다른 글
| 13. 논리회로 - 플립플롭(Flip-Flop) (4) | 2021.08.09 |
|---|---|
| 12. 논리회로 - 조합논리회로 (0) | 2021.08.06 |
| 10. 논리회로 - 부울대수와 논리식의 간편화 (0) | 2021.08.05 |
| 9. 논리회로 - 논리 게이트(logical gate) (1) | 2021.08.05 |
| 8. 데이터 표현 - BCD, 패리티 비트, 해밍코드 (0) | 2021.08.05 |




댓글