0. 시작하기 전에
지금까지 공부한 내용을 쭉 복습해보자.
- 컴퓨터에서 수를 표현하고 계산하는 방법에 대해서 알아보았다.
- 여러가지 진법과, 보수를 이용한 음수를 계산하는 방법을 다루었다.
- 이진법에서 사용하는 1의 보수와 2의 보수를 배웠고,
- 왜 2의 보수를 사용하는지에 대해서 알게 되었다.
- 컴퓨터가 수를 계산하는 과정을 논리회로의 관점에서 알아보았다.
- 부울 대수와 진리표를 이용해서 논리 회로를 그리는 방법과 논리 회로를 논리식으로 표현하는 방법을 배웠다.
- 논리식을 더욱 간단하게 구하기 위해, 카르노맵을 사용하여 진리표를 만들고 이를 이용해 논리식을 계산하는 방법까지 공부했다.
위에서 말한 모든 것을 사용하여 조합논리회로를 만든다.
조합논리회로란, 입력값을 기반으로 어떤 결과값을 계산하는 기능을 하는 회로를 의미한다.
그러나 조합논리회로만을 이용해서 컴퓨터를 구성할 수 없다. 왜냐면 기억 회로가 필요하기 때문이다.
이번 포스팅은 컴퓨터를 구성하는 조합논리회로와 기억 회로에 대해서,
그리고 이 모든 것을 갖춘 순차 회로에 대해 알아보도록 하자.
1. 조합논리회로와 기억 회로의 형태
- 조합논리회로는 입력과 출력을 가진 논리 게이트의 집합이다.
- 순차논리 회로는 게이트 뿐만 아니라 기억능력이 있는 기억회로(Flip-Flop)로 구성된다.
- 즉, 순차논리회로가 제대로된 논리회로의 최종형태라는 것을 알아두자.

2. 대표적인 조합논리회로
a) 전가산기(Full Adder)
- 캐리를 포함한 두자리 이상의 비트 계산이 가능한 계산기를 말한다.
- 즉, 1(캐리) + 1 + 1 또는 1 + 1, 1 + 0, 0 + 1 등의 계산이 가능하다.
- 이와 같은 이유로 전가산기는 3개의 입력을 갖는다는 특징이 있다.
b) 반가산기(Half Adder)
- 캐리를 제외한 두자리 비트계산만이 가능한 계산기를 말한다.
- 다시 말하자면, 캐리비트가 발생하는 연산은 수행할 수 없다.
- 즉, 0 + 1 또는 1 + 0 연산만이 가능하다.
3. 반가산기 회로를 만들어보자.
a) 반가산기 진리표 계산
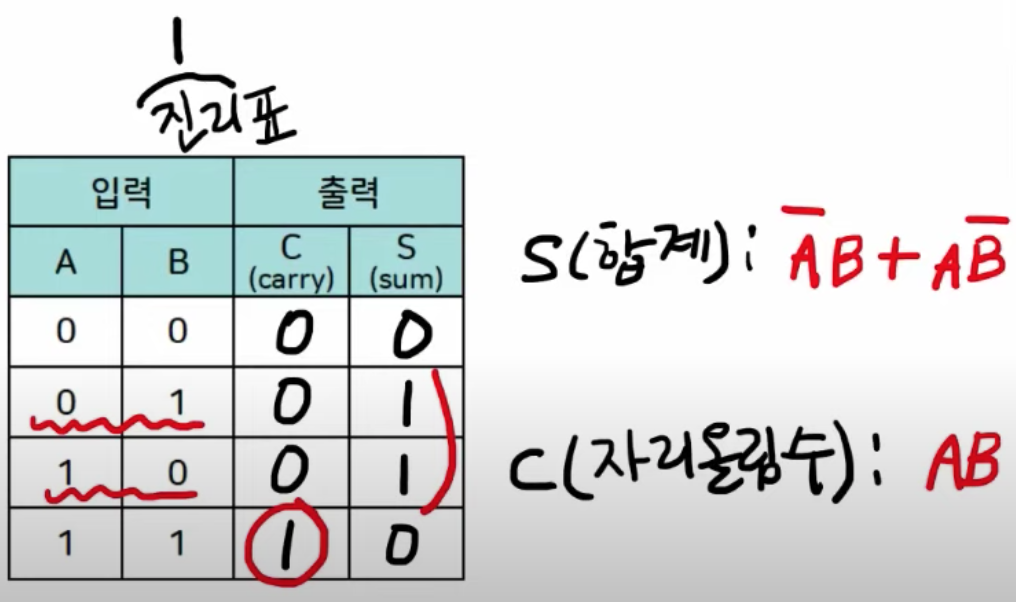
- 우선, 진리표는 진리를 표시하기 위한 표이다. 즉, 1을 표시하기 위한 표이다.
- 이 진리표를 계산하면 위의 그림과 같이 계산결과가 나오는 것을 알 수 있다.
- 이를 바탕으로 캐리와 합(Sum)에 대한 각각의 진리표를 그리면 다음과 같이 나온다.

- 합과 캐리에 대한 연산값을 진리표에 표시하면 위와 같다.
- 합은 exclusive or 게이트와 동일한 형태를 취한다.
- 캐리는 and 게이트와 동일한 형태를 취한다.
- 이를 통해서 반가산기는 A, B 두개의 입력에 대해 XoR과 AND 게이트 각 1개씩을 필요로 한다는 것을 알 수 있다.
- 이를 회로도로 그리면 다음과 같다.

- 반가산기는 XoR과 AND 게이트를 각 1개씩 필요로 한다.
- 이 뜻은 모든 가산기는 반드시 XoR과 AND 게이트를 1개씩 필요로 한다는 전제가 된다.
- 다시 말하자면, 가산기의 기본 회로는 XoR 과 AND 게이트를 1개씩 갖는다는 것이다.
4. 전가산기 회로를 만들어보자.
a)전가산기 진리표 계산
- 반가산기와 동일한 방법으로 전가산기의 회로를 그려보자.
- 전가산기의 진리표를 작성하면 다음과 같이 계산할 수 있다.
1) 전가산기의 합(sum)

- sum에서 1을 반환한 부분의 입력값을 가지고 논리식을 작성한다.
- 위의 사진과 같이 일련의 과정을 통해 전가산기의 합을 구한다.
2) 전가산기의 캐리

- 전가산기의 합을 구한 것과 동일한 방식으로 캐리 값을 구한다.
3) 전가산기의 회로도
- 여기서 조금 헷갈려하는 분들을 위해 한가지 개념을 설명하고자 한다.
- 논리 합(= 합집합)은 OR
- 논리 곱(= 교집합)은 AND
- 배타적 논리합(= 합집합에서 교집합을 제외한 집합)은 XoR
- 위의 계산된 S와 C를 이용하여 회로도를 그리면 다음과 같다.

- 이를 통해, 전가산기는 2개의 반가산기와 1개의 OR 게이트의 조합이라는 것을 알 수 있다.
* 반가산기는 XoR 게이트와 AND 게이트를 1개씩 갖는다.
[자료출처]
'컴퓨터공학기초 개념 > 컴퓨터구조' 카테고리의 다른 글
| 14. CPU 내부구조 - 레지스터 (0) | 2021.08.10 |
|---|---|
| 13. 논리회로 - 플립플롭(Flip-Flop) (4) | 2021.08.09 |
| 11. 논리회로 - 카르노맵(karnaugh map) (0) | 2021.08.06 |
| 10. 논리회로 - 부울대수와 논리식의 간편화 (0) | 2021.08.05 |
| 9. 논리회로 - 논리 게이트(logical gate) (1) | 2021.08.05 |




댓글